% Research @ Mangaki % Jill-Jênn Vie % RIKEN Center for Advanced Intelligence Project (Tokyo)\newline Mangaki (Paris) — header-includes: - \usepackage{tikz} - \usepackage{array} - \usepackage{icomma} - \usepackage{multicol,booktabs} - \def\R{\mathcal{R}} handout: true —

Jill-Jênn Vie

• 2006: Prépa MP au lycée Thiers
• 2008: Auditeur 1A à l’ENS de Lyon \hfill (pavages, Markov)
• 2010: Normalien 3A à l’ENS Paris-Saclay \hfill (langages, crypto)
• 2012: Master Parisien de Recherche Informatique \hfill (crypto)
• 2013: Raté un master de mathématiques (MVA) \hfill (Akinator)
• 2014: Agrégation de mathématiques \hfill (géo diff)
• 2016: Thèse d’informatique à Paris-Saclay \hfill (active learning)
• 2017: Postdoc à Tokyo \hfill (crowdsourcing)

RIKEN Center for Advanced Intelligence Project

\

• RIKEN is the biggest public research institution in Japan
• New AI lab near Tokyo Station (opened in 2016)
• 3 interns from Master Vision Apprentissage in ENS Paris-Saclay
• 8 accepted papers at NIPS 2017

Outline

Deep Learning

• history
• word2vec
• images

Recommendation Systems

• KNN
• ALS
• Hybrid

Further work

• Privacy
• Bias
• Extra sources of information

Deep Learning

• 1957 : Perceptron : le premier réseau de neurones
• 1969 : Minsky met en évidence des limitations $\rightarrow$ perte de fonds

Trio conspirationniste

Geoffrey Hinton (Canadien @ Univ. Toronto & Google Brain)
Yann LeCun (Français @ Facebook AI Research), son postdoc Yoshua Bengio (Français @ Univ. Montréal), son postdoc

\pause

• 2007 : fake workshop organisé à NIPS
• 2012 : breakthrough traitement du langage
• 2015 : breakthrough reconnaissance d’images
• 2017 : $$$

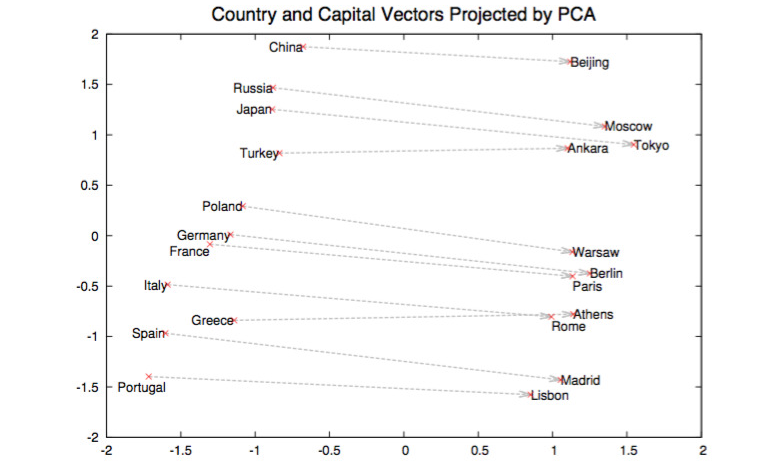
word2vec (Mikolov et al., 2013)

• word $\rightarrow \mathbb{R}^d$
• document $\rightarrow$ mean of vectors of words

\

Also: $king - man + woman = queen$.

images2vec

\

Image recognition

\centering

\
\

Image captioning

\

Image captioning + attention (Xu and Bengio, 2015)

\

Translation + attention

\centering

\

Generative Adversarial Networks (Goodfellow, 2014)

\

Article cité 1340 fois.

Image interpolation

\centering

\

MakeGirls.Moe (Jin et al., 2017)

\

Recommender systems

Problem

• Every user rates few items (1 %)
• How to infer missing ratings?

\begin{tabular}{ccccc} & \includegraphics[height=2.5cm]{figures/1.jpg} & \includegraphics[height=2.5cm]{figures/2.jpg} & \includegraphics[height=2.5cm]{figures/3.jpg} & \includegraphics[height=2.5cm]{figures/4.jpg}
Sacha & ? & 5 & 2 & ?
Ondine & 4 & 1 & ? & 5
Pierre & 3 & 3 & 1 & 4
Joëlle & 5 & ? & 2 & ? \end{tabular}

Filtrage collaboratif

\begin{tabular}{ccccc} & \includegraphics[height=2.5cm]{figures/1.jpg} & \includegraphics[height=2.5cm]{figures/2.jpg} & \includegraphics[height=2.5cm]{figures/3.jpg} & \includegraphics[height=2.5cm]{figures/4.jpg}
Sacha & \alert{3} & 5 & 2 & \alert{2}
Ondine & 4 & 1 & \alert{4} & 5
Pierre & 3 & 3 & 1 & 4
Joëlle & 5 & \alert{2} & 2 & \alert{5} \end{tabular}

Every supervised machine learning algorithm

fit($X$, $y$)

\centering \begin{tabular}{ccc} \toprule \multicolumn{2}{c}{$X$} & $y$\ \cmidrule{1-2} \texttt{user_id} & \texttt{work_id} & \texttt{rating}\ \midrule 24 & 823 & like
12 & 823 & dislike
12 & 25 & favorite
\ldots & \ldots & \ldots\ \bottomrule \end{tabular}

\pause

$\hat{y}$ = predict($X$)

\centering \begin{tabular}{ccc} \toprule \multicolumn{2}{c}{$X$} & $\hat{y}$\ \cmidrule{1-2} \texttt{user_id} & \texttt{work_id} & \texttt{rating}\ \midrule 24 & 25 & \only<2>{?}\only<3>{\alert{disliked}}
12 & 42 & \only<2>{?}\only<3>{\alert{liked}}\ \bottomrule \end{tabular}

Algorithme des plus proches voisins

Pour recommander des films à quelqu’un :

• On introduit un \alert{score de similarité} entre personnes
• On détermine les 10 personnes \alert{les plus proches} de lui
• On lui recommande ce qu’ils ont aimé qu’il n’a pas vu

Nos données

\begin{tabular}{c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c} & \footnotesize{007} & \footnotesize{Batman 1} & \footnotesize{Shrek 2} & \footnotesize{Toy Story 3} & \footnotesize{Star Wars 4} & \footnotesize{Twilight 5}
Alice & $+$ & $-$ & $0$ & $+$ & $0$ & $-$
Bob & $-$ & $0$ & $+$ & $-$ & $+$ & $+$
Charles & $+$ & $+$ & $+$ & $+$ & $-$ & $-$
Daisy & $+$ & $+$ & $0$ & $0$ & $+$ & $-$
Everett & $+$ & $-$ & $+$ & $+$ & $-$ & $0$
\end{tabular}

\begin{center} Quel score de similarité entre utilisateurs choisir ? \end{center}

Calcul du score

\begin{tabular}{c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c} & \footnotesize{007} & \footnotesize{Batman 1} & \footnotesize{Shrek 2} & \footnotesize{Toy Story 3} & \footnotesize{Star Wars 4} & \footnotesize{Twilight 5}
Alice & $+$ & $-$ & $0$ & $+$ & $0$ & $-$
Charles & $+$ & $+$ & $+$ & $+$ & $-$ & $-$
Score & $+1$ & $-1$ & & $+1$ & & +1
\end{tabular} \vspace{-1mm} \begin{center} $score(\textnormal{Alice}, \textnormal{Charles}) = 3 + (-1) = \alert{2}$
\end{center} \vspace{2mm}

\begin{tabular}{c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c} & \footnotesize{007} & \footnotesize{Batman 1} & \footnotesize{Shrek 2} & \footnotesize{Toy Story 3} & \footnotesize{Star Wars 4} & \footnotesize{Twilight 5}
Alice & $+$ & $-$ & $0$ & $+$ & $0$ & $-$
Bob & $-$ & $0$ & $+$ & $-$ & $+$ & $+$
Score & $-1$ & & & $-1$ & & -1
\end{tabular} \vspace{-1mm} \begin{center} $score(\textnormal{Alice}, \textnormal{Bob}) = \alert{-3}$\bigskip \vspace{2mm}

Alice est \alert{plus proche} de Charles que de Bob \end{center}

Score de similarité entre personnes

\begin{center} \begin{tabular}{c@{\hspace{2mm}}|c@{\hspace{2mm}}c@{\hspace{2mm}}c@{\hspace{2mm}}c@{\hspace{2mm}}c} & Alice & Bob & Charles & Daisy & JJ
\hline Alice & $4$ & $-3$ & $2$ & $1$ & $3$
Bob & $-3$ & $5$ & $-3$ & $-1$ & $-2$
Charles & $2$ & $-3$ & $6$ & $2$ & $3$
Daisy & $1$ & $-1$ & $2$ & $4$ & $-1$
Everett & $3$ & $-2$ & $3$ & $-1$ & $5$
\end{tabular} \end{center}

\begin{center} Qui sont les 2 plus proches voisins d’Alice ? \end{center}

Evaluation: Root Mean Squared Error (RMSE)

If I predict $\hat{y_i}$ for each user-work pair to test among $n$,
while truth is $y^*_i$:

\[RMSE(\hat{y}, y^*) = \sqrt{\frac1n \sum_i (\hat{y}_i - y^*_i)^2}.\]

Dataset: Mangaki

\

• 2300 users
• 15000 works \textcolor{gray}{\hfill {\em \small anime / manga / OST}}
• 340000 ratings \textcolor{gray}{\hfill {\em \small fav / like / dislike / neutral / willsee / wontsee}}
• User can rate anime or manga
• And receive recommendations
• And reorder their watchlist

\pause

• Code is 100% on GitHub
• Awards from Microsoft and Japanese Foundation
• Made a data challenge with Kyoto U! research.mangaki.fr

Recommendation algorithms

Content-based

(features for movies: directors, genre, etc.)

Collaborative filtering

(solely based on ratings)

Hybrid recommender systems

(combine those two)

KNN $\rightarrow$ measure similarity between users (or items)

$K$-nearest neighbors

• $\R_u$ represents the row vector of user $u$ in the rating matrix (users $\times$ works).
• Similarity score between users (cosine): \(score(u, v) = \frac{\R_u \cdot \R_v}{||\R_u|| \cdot ||\R_v||}.\)
• Let’s identify the $k$-nearest neighbors of user $u$
• And recommend to user $u$ what $u$’s neighbors liked
  but $u$ didn’t see

Hint

If $R’$ the $N \times M$ matrix of rows $\frac{\R_u}{

\R_u

}$, we can get the $N \times N$ score matrix by computing $R’ R’^T$.

Matrix factorization $\rightarrow$ reduce dimension to generalize

\vspace{-7mm}

\(R = \left(\begin{array}{c} \R_1\\ \R_2\\ \vdots\\ \R_n \end{array}\right) = \raisebox{-1cm}{\begin{tikzpicture} \draw (0,0) rectangle (2.5,2); \end{tikzpicture}} = \raisebox{-1cm}{\begin{tikzpicture} \draw (0,0) rectangle ++(1,2); \draw node at (0.5,1) {$C$}; \draw (1.1,1) rectangle ++(2.5,1); \draw node at (2.35,1.5) {$P$}; \end{tikzpicture}}\) \(\text{$R$: 2k users $\times$ 15k works} \iff \left\{\begin{array}{l} \text{$C$: 2k users $\times$ \alert{20 profiles}}\\ \text{$P$: \alert{20 profiles} $\times$ 15k works}\\ \end{array}\right.\) $\R_\text{Bob}$ is a linear combination of profiles $P_1$, $P_2$, etc..

\pause

Interpreting Key Profiles

\begin{tabular}{@{}lccc@{}} If $P$ & $P_1$: adventure & $P_2$: romance & $P_3$: plot twist
And $C_u$ & $0,2$ & $-0,5$ & $0,6$ \end{tabular}

$\Rightarrow$ $u$ \alert{likes a bit} adventure, \alert{hates} romance, \alert{loves} plot twists.

\vspace{2mm}

\pause

Ex. Singular Value Decomposition (SVD)

$R = (U \cdot \Sigma)V^T$ where $U : N \times r$ et $V : M \times r$ are orthogonal and $\Sigma : r \times r$ is diagonal, with singular values in decreasing order.

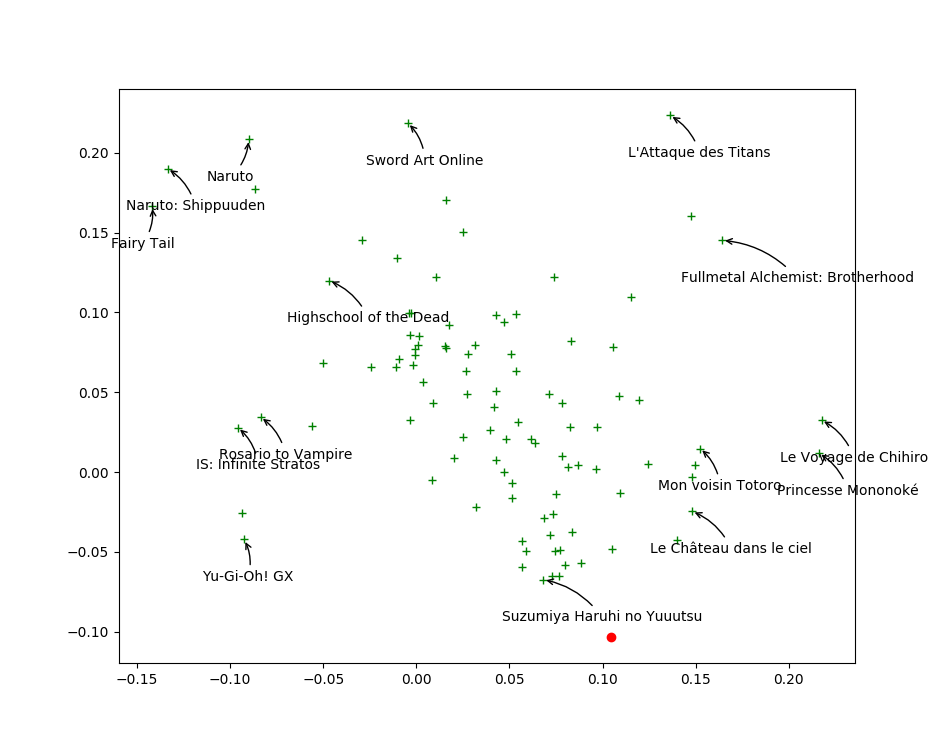
Visualizing first two columns of $V_j$ in SVD

\alert{Closer} points mean similar taste

\

Find your taste by plotting first two columns of $U_i$

You will \alert{like} movies that are \alert{in your direction}

\

Variants of Matrix Factorization for Recommendation

$R$ ratings, $C$ coefficients, $P$ profiles ($F$ features).

$R = CP = CF^T \Rightarrow r_{ij} \simeq \hat{r}_{ij} \triangleq C_i \cdot F_j$.

Objective functions (reconstruction error) to minimize

SVD : $\sum_{i, j}~(r_{ij} - C_i \cdot F_j)^2$ (deterministic)

\pause

ALS : $\sum_{i, j \textnormal{\alert{ known}}}~(r_{ij} - C_i \cdot F_j)^2$

\pause

\alert<6>{ALS-WR} : $\sum_{i, j \textnormal{\alert{ known}}}~(r_{ij} - C_i \cdot F_j)^2 + \lambda (\sum_i \alert<6>{N_i} ||C_i||^2 + \sum_j \alert<6>{M_j} ||F_j||^2)$
where $N_i$ ($M_j$): how many times user $i$ rated (item $j$ was rated)

\pause

WALS by Tensorflow™ : \(\sum_{i, j} w_{ij} \cdot (r_{ij} - C_i \cdot F_j)^2 + \lambda (\sum_i ||C_i||^2 + \sum_j ||F_j||^2)\)
where $w_{ij}$: how much can you trust rating $r_{ij}$.

\pause

Who do you think wins?

ALS for feature extraction

$R = CP$

Issue: Item Cold-Start

• If no ratings are available for an anime
  $\Rightarrow$ no feature will be trained
• If anime features at put to 0
  $\Rightarrow$ prediction of ALS will be constant for every unrated anime.

\pause

But we have posters!

• On Mangaki, almost all works have a poster
• How to extract information?

Illustration2Vec (Saito and Matsui, 2015)

\centering

{width=40%}\ {width=40%}\

• CNN (VGG-16) pretrained on ImageNet, trained on Danbooru
  (1.5M illustrations with tags)
• 502 most frequent tags kept, outputs \alert{tag weights}

Ce que les stagiaires ont fait avec Illustration2Vec

\

Ce que les stagiaires ont fait avec Illustration2Vec II

\

Blended Alternate Least Squares with Explanation

\centering

LASSO for explanation of user preferences

$T$ matrix of 15000 works $\times$ 502 tags ($t_{jk}$: tag $k$ appears in item $j$)

• Each user is described by its preferences $P_i$
  $\rightarrow$ a \alert{sparse} row of weights over tags.
• Estimate user preferences $P_i$ such that $r_{ij} \simeq P_iT_j^T$.

\pause

Least Absolute Shrinkage and Selection Operator (LASSO)

\[\frac1{2 N_i} {\lVert \R_i - P_i T^T \rVert}_2^2 + \alpha \alert{ {\lVert P_i \rVert}_1}.\]

\noindent where $N_i$ is the number of items rated by user $i$.

\pause

Interpretation and explanation

• You seem to like \alert{\emph{magical girls}} but not \alert{\emph{blonde hair}}
  $\Rightarrow$ Look! All of them are \alert{\emph{brown hair}}! Buy now!

Blending

We would like to do:

\[\hat{r}_{ij}^{BALSE} = \begin{cases} \hat{r}_{ij}^{ALS} & \text{if item $j$ was rated at least $\gamma$ times}\\ \hat{r}_{ij}^{LASSO} & \text{otherwise} \end{cases}\]

But we can’t. Why? \pause \alert{Not differentiable!}

\[\hat{r}_{ij}^{BALSE} = \alert{\sigma(\beta(R_j - \gamma))} \hat{r}_{ij}^{ALS} + \left(1 - \alert{\sigma(\beta(R_j - \gamma))}\right) \hat{r}_{ij}^{LASSO}\]

\noindent where $R_j$ denotes how many times item $j$ was rated
$\beta$ and $\gamma$ are learned by stochastic gradient descent.

\pause

\centering

We call this gate the \alert{Steins;Gate}.

Blended Alternate Least Squares with Explanation

\centering

\

\pause

We call this model \alert{BALSE}.

Results

\centering

\

Further Work

Privacy

Si on apprend un modèle génératif (type GAN) à générer des fake ratings
On peut ouvrir notre dataset sans risquer que les gens soient identifiés

Bias

Existe-t-il une minorité (ex. filles) insatisfaite sur Mangaki ?

Intégrer des sources d’informations extérieures

Wikidata, TV Tropes, AniDB, etc.

Thank you!

\centering {width=50%}\

\raggedright

Read the article

\small Using Posters to Recommend Anime and Mangas in a Cold-Start Scenario

\normalsize \alert{github.com/mangaki/balse} (PDF on arXiv, front page of HNews)

Mangaki Data Challenge: \alert{research.mangaki.fr}

• Who won? Japan? France? US? Korea? \alert<2>{China?} You?

Try it: \alert{https://mangaki.fr} \newline Twitter: \alert{@MangakiFR}