% Learning Fair Representations % JJV % \Large Link to paper — hyperrefoptions: colorlinks header-includes: - \usepackage{tikz} —

Fairness

“Different models with the same reported accuracy can have a very different distribution of error across population” (Hardt, 2017)

\pause

Crime prediction (watch Psycho-Pass):

Goals

• \alert{Group fairness}: positive rate in group $\simeq$ positive rate overall
• \alert{Individual fairness}: similar people receive similar outcomes
• Find a trade-off between accuracy and fairness

This paper: “Fairness regularizer”

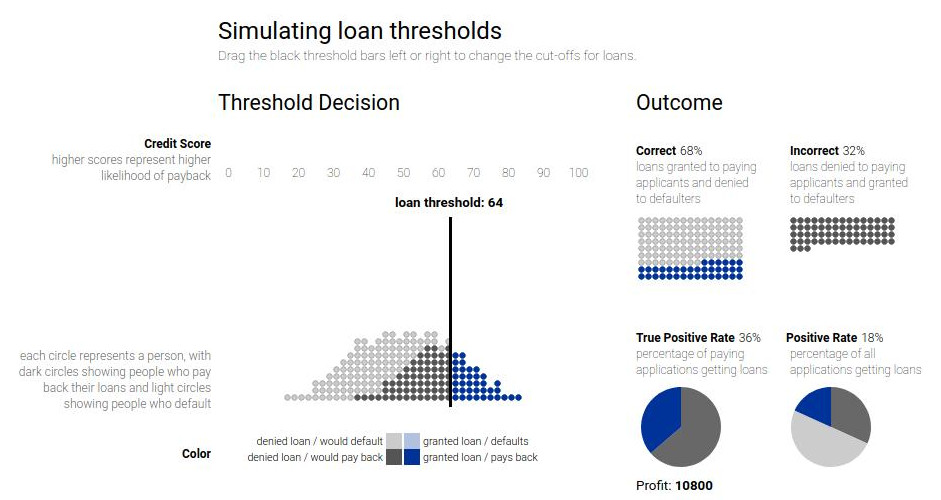
Example of fairness

\centering

{width=100%}

See Attacking discrimination with smarter machine learning

Visually

\centering

Formally

\[M_{n, k} = P(Z = k|x_n) \propto \exp(-d(x_n, \alert{v_k}))\]

\raggedleft High if $x_n$ is close to $\alert{v_k}$

\raggedright

\[\hat{x_n} = \sum_k M_{n, k} \alert{v_k}\]

\only<1>{\(\displaystyle \widehat{y_n} = \sum_k M_{n, k} \alert{w_k}\)} \only<2>{\(\widehat{y_n} = \sum_k \underbrace{M_{n, k}}_{\in \{0, 1\}} \alert{w_k}\)} \only<3>{\(\widehat{y_n} = \sum_k \underbrace{M_{n, k}}_{\in \{0, 1\}} \underbrace{\alert{w_k}}_{\in \{0, 1\}}\)}

$\alert{v_k} \in \mathbf{R}^d$, $\alert{w_k} \in \mathbf{R}$ are \alert{learned}

Objective

Accuracy

$L_y = \sum_n - y_n \log \hat{y_n} - (1 - y_n) \log (1 - \hat{y_n})$

Reconstruction

$L_x = \sum_n

x_n - \hat{x}_n

^2$

Fairness

$L_z = \sum_k

M_k^+ - M_k^-

$

where $M_k^+ = \underbrace{\mathbb{E}+ M{n, k}}_{\textnormal{average across subgroup}}$

\only<1>{\(L = A_z L_z + A_x L_x + A_y L_y\)} \only<2>{\(L = A_z L_z + A_x L_x + A_y \alert{N_D}\)}

Baselines

LR: Logistic Regression

FNB: Fair Naive Bayes

RLR: Regularized LR

LFR: Learning Fair Representations

Results I

Accuracy (high)

Discrimination (low)

\[D = | \mathbb{E}_+ \hat{y}^n - \mathbb{E}_- \hat{y}^n |\]

Results I, see paper

\centering

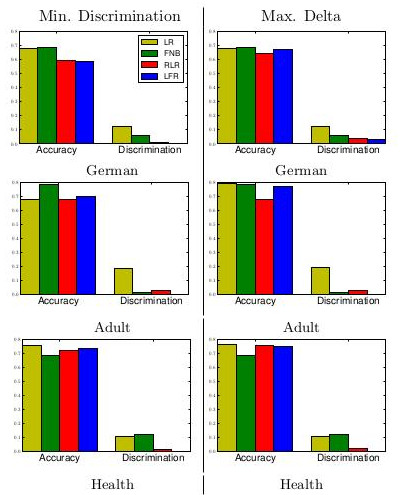{width=70%}

Results II

Consistency (high)

\[y_{nn} = 1 - \frac1{Nk} \sum_n \left| \hat{y}_n - \sum_{j \in kNN(x_n)} \hat{y}_j \right|\]

Results II

\centering

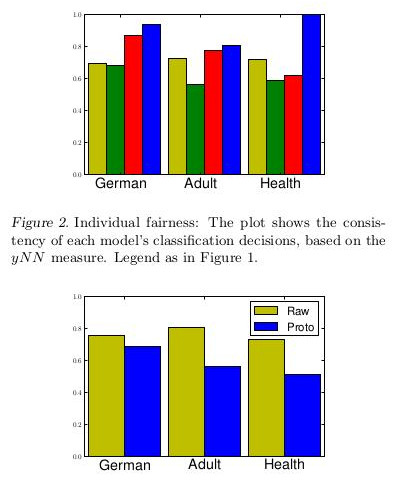{width=60%}

Going beyond: AUC constraints

Constraints on AUC or area between ROC curves (ABROCA)

\centering

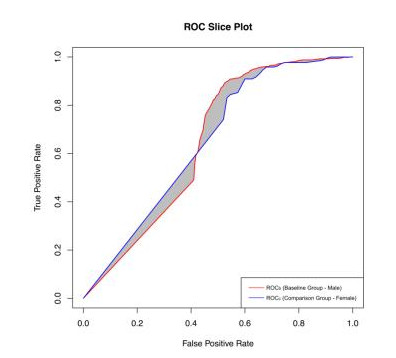{width=60%}

\raggedright

Evaluating the Fairness of Predictive Student Models Through Slicing Analysis (Gardner, Brooks and Baker, 2019)

Also works from Bellet next door

Going beyond: Relation to differential privacy

\centering

{width=60%}

\pause

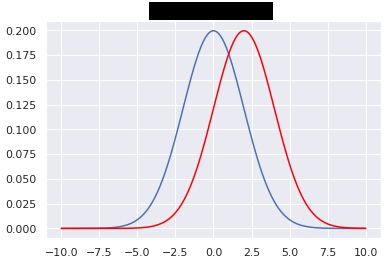
\[\begin{aligned} \forall S \subset \textnormal{Im} A, \forall D_1, D_2 \textnormal{"close"}, Pr(A(D_1) \subset S) \leq e^\varepsilon Pr(A(D_2) \subset S)\\ \forall S \subset \textnormal{Im} A, \forall D_1, D_2 \textnormal{"close"} \left|\frac{\log Pr(A(D_1) \in S)}{\log Pr(A(D_2) \in S)}\right| \leq \varepsilon \end{aligned}\]

\raggedright

For more on this beautiful relationship:
Fairness through Awareness (Dwork et al., 2011)