Jill-Jênn Vie

Researcher at Inria

% Knowledge Tracing Machines:\newline Factorization Machines for Knowledge Tracing % Jill-Jênn Vie; Hisashi Kashima % The University of Tokyo, February 7, 2019\bigskip\newline \url{https://arxiv.org/abs/1811.03388} — theme: Frankfurt handout: false institute: \includegraphics[height=9mm]{figures/aip-logo.png} \quad \includegraphics[height=1cm]{figures/kyoto.png} section-titles: false biblio-style: authoryear header-includes: - \usepackage{booktabs} - \usepackage{multicol,multirow} - \usepackage{algorithm,algpseudocode} - \usepackage{bm} - \usepackage{tikz} - \DeclareMathOperator\logit{logit} - \def\ReLU{\textnormal{ReLU}} - \def\correct{\includegraphics{figures/win.pdf}} - \def\mistake{\includegraphics{figures/fail.pdf}} - \DeclareMathOperator\probit{probit} - \usepackage{newunicodechar} - \DeclareRobustCommand{\okina}{\raisebox{\dimexpr\fontcharht\fontA-\height}{\scalebox{0.8}{}}} - \newunicodechar{ʻ}{\okina} biblatexoptions: - maxbibnames=99 - maxcitenames=5 —

Introduction

Who is this person?

\centering

\includegraphics[width=0.42\linewidth]{figures/gan0.png}

… Actually, she does not exist

\

\centering 5 years of GAN progress on face generation

\raggedright A Style-Based Generator Architecture for Generative Adversarial Networks (Karras, Laine and Aila, 2018) arxiv.org/abs/1812.04948

AI for Social Good

\begin{columns} \begin{column}{0.5\linewidth} AI can: \begin{itemize} \item generate fakes \item recognize images/speech \item predict the next word \item play go (make decisions) \end{itemize} as long as you have enough data. \end{column} \begin{column}{0.5\linewidth} Can it also: \begin{itemize} \item generate exercises \item \alert{improve education} \item \alert{predict student performance} \item optimize human learning \end{itemize} as long as you have enough data? \end{column} \end{columns}

My research

Use machine learning techniques on data that comes from humans

Outline

  1. Introduction to machine learning

  2. Knowledge Tracing and existing models

  3. Knowledge Tracing Machines
    • Encoding data into sparse features
    • Running logistic regression or factorization machines
  4. Experiments and results

What is machine learning?

Train a model on some data (e.g. pictures of cats)
Test it on new data
Tweak the parameters to optimize a value (e.g., maximize accuracy)

How to choose the best model?

Train model on some of your data, keep the remaining data hidden Try to predict the remaining data

What is a good machine learning model?

Can reconstruct training data at 90%
predicts new points correctly 80% of the time

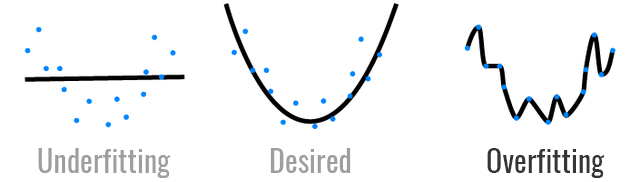
What is a bad machine learning model?

Can reconstruct training data at 100%
predicts new points correctly 20% of the time

It is called overfitting

\centering \includegraphics[width=5cm]{figures/overfit.png}

\

Formally

We have existing data $(\bm{x}, y)$
and we want to learn a function $y = f(\bm{x})$.

\begin{exampleblock}{Examples} \begin{minipage}{0.15\linewidth} ~ \end{minipage} \begin{minipage}{0.75\linewidth} \begin{itemize} \item[classification] $\bm{x}$ can be an image and $y \in {man, woman}$ \item[regression] $\bm{x}$ can be the temperature over the last 7 days and $y$ is the temperature of the next day \end{itemize} \end{minipage} \end{exampleblock}

Two typical examples

For regression: \alert{linear regression}

We have existing data $(\bm{x}, y) \in \mathbb{R}^d \times \mathbb{R}$ and we want to learn a function $y = \langle \alert{\bm{w}}, \bm{x} \rangle + \alert{b} = \sum_i w_i x_i + b$.

Example if $d = 1$: we want to learn $\alert{w} x + \alert{b} = y$, an affine function!\vspace{5mm}

\pause

For classification: \alert{logistic regression}

We have existing data $(\bm{x}, y) \in \mathbb{R}^d \times {0, 1}$ and we want to learn a function $y = \sigma(\langle \alert{\bm{w}}, \bm{x} \rangle + \alert{b})$.

\begin{tikzpicture} \draw[->,black] (0,0) – (3,0) node[below] {$h$}; \draw[->,black] (0,0) – (0,1.5) node[left] {$y$}; \draw (2pt,1) – ++(-4pt,0) node[left] {1}; \draw[blue,smooth,thick] plot[id=f1,domain=-3:3,samples=50] ({\x,{1/(1+exp(-\x))}}) node[above] {sigmoid: $\sigma : h \mapsto 1/(1 + \exp(-h))$}; \end{tikzpicture}

Is accuracy a good metric for classification?

\pause

If 99% of people are in good health, and you are making a machine learning algorithm that \alert{always} predicts a person is healthy…
It will have accuracy 99%.

Is this a good machine?

Better metrics: AUC, F1 score, etc.

Knowledge Tracing

Students try exercises

Math Learning

\centering \begin{tabular}{cccc} \toprule Items & 5 – 5 = ? & \only<2->{17 – 3 = ?} & \only<3->{13 – 7 = ?}\ \midrule New student & \alert{$\circ$} & \only<2->{\alert{$\circ$}} & \only<3->{\alert{$\mathbf{\times}$}}\ \bottomrule \end{tabular}

\raggedright \only<4->{Language Learning

\includegraphics{figures/duolingo0.png}}

\pause\pause\pause\pause

Challenges

Predicting student performance: knowledge tracing

Data

A population of users answering items

Side information

Goal: classification problem

Predict the performance of new users on existing items

Method

Learn parameters of questions from historical data \hfill \emph{e.g., difficulty}
Measure parameters of new students \hfill \emph{e.g., expertise}

Existing work {.fragile}

\footnotesize \begin{tabular}{cccc} \toprule \multirow{2}{}{Model} & \multirow{2}{}{Basically} & Original & \only<3->{Fixed}
& & AUC & \only<3->{AUC}\ \midrule Bayesian Knowledge Tracing & \multirow{2}{}{Hidden Markov Model} & \multirow{2}{}{0.67} & \only<3->{\multirow{2}{}{0.63}}
(\cite{corbett1994knowledge})\ \midrule \only<2->{Deep Knowledge Tracing & \multirow{2}{}{Recurrent Neural Network} & \multirow{2}{}{0.86} & \only<3->{\multirow{2}{}{0.75}}\} \only<2->{(\cite{piech2015deep})\ \midrule} \only<4->{Item Response Theory & \multirow{3}{}{Online Logistic Regression} & \multirow{3}{}{} & \multirow{3}{*}{0.76}\} \only<4->{(\cite{rasch1960studies})\} \only<4->{(Wilson et al., 2016) \ \bottomrule} \end{tabular}

\only<5>{\(\underbrace{\textnormal{PFA}}_{\textnormal{LogReg}} \! \leq \underbrace{\textnormal{DKT}}_{\textnormal{LSTM}} \leq \! \underbrace{\textnormal{IRT}}_{\textnormal{LogReg}} \! \alert{\leq \underbrace{\textnormal{KTM}}_{\textnormal{FM}}}\)}

Limitations and contributions

In this paper

Encoding existing models

Our small dataset

\begin{columns} \begin{column}{0.6\linewidth} \begin{itemize} \item User 1 answered Item 1 correct \item User 1 answered Item 2 incorrect \item User 2 answered Item 1 incorrect \item User 2 answered Item 1 correct \item User 2 answered Item 2 ??? \end{itemize} \end{column} \begin{column}{0.4\linewidth} \centering \input{tables/dummy-ui-weak}\vspace{5mm}

\texttt{dummy.csv} \end{column} \end{columns}

Our approach

\includegraphics[width=\linewidth]{figures/archi.pdf}

Model 1: Item Response Theory

Learn abilities $\alert{\theta_i}$ for each user $i$
Learn easiness $\alert{e_j}$ for each item $j$ such that: \(\begin{aligned} Pr(\textnormal{User $i$ Item $j$ OK}) & = \sigma(\alert{\theta_i} + \alert{e_j}) \quad \sigma : x \mapsto 1/(1 + \exp(-x))\\ \logit Pr(\textnormal{User $i$ Item $j$ OK}) & = \alert{\theta_i} + \alert{e_j} \end{aligned}\)

Really popular model, used for the PISA assessment

Logistic regression

Learn $\alert{\bm{w}}$ such that $\logit Pr(\bm{x}) = \langle \alert{\bm{w}}, \bm{x} \rangle + b$

Graphically: IRT as logistic regression

Encoding “User $i$ answered Item $j$” with \alert{sparse features}:

\centering

\[\langle \bm{w}, \bm{x} \rangle = \theta_i + e_j = \logit Pr(\textnormal{User $i$ Item $j$ OK})\]

Encoding into sparse features

\centering

\input{tables/show-ui}

\raggedright Then logistic regression can be run on the sparse features.

Oh, there’s a problem

\input{tables/pred-ui}

We predict the same thing when there are several attempts.

Count number of attempts: AFM

Keep a counter of attempts at skill level:

\centering

\input{tables/dummy-uisa}

Count successes and failures: PFA

Count separately successes $W_{ik}$ and fails $F_{ik}$ of student $i$ over skill $k$.

\centering

\input{tables/dummy-uiswf}

Model 2: Performance Factor Analysis

$W_{ik}$: how many successes of user $i$ over skill $k$ ($F_{ik}$: #failures)

Learn $\alert{\beta_k}$, $\alert{\gamma_k}$, $\alert{\delta_k}$ for each skill $k$ such that: \(\logit Pr(\textnormal{User $i$ Item $j$ OK}) = \sum_{\textnormal{Skill } k \textnormal{ of Item } j} \alert{\beta_k} + W_{ik} \alert{\gamma_k} + F_{ik} \alert{\delta_k}\)

\centering \input{tables/show-swf}

Better!

\input{tables/pred-swf}

Test on a large dataset: Assistments 2009

346860 attempts of 4217 students over 26688 items on 123 skills.

\vspace{1cm}

\centering \input{tables/assistments42-afm-pfa}

Knowledge Tracing Machines

Model 3: a new model (but still logistic regression)

\input{tables/assistments42-afm-pfa-iswf}

Here comes a new challenger

How to model \alert{pairwise interactions} with \alert{side information}?

Logistic Regression

Learn a 1-dim \alert{bias} for each feature (each user, item, etc.)

Factorization Machines

Learn a 1-dim \alert{bias} and a $k$-dim \alert{embedding} for each feature

How to model pairwise interactions with side information?

If you know user $i$ attempted item $j$ on \alert{mobile} (not desktop)
How to model it?

$y$: score of event “user $i$ solves correctly item $j$”

IRT

\[y = \theta_i + e_j\]

Multidimensional IRT (similar to collaborative filtering)

\[y = \theta_i + e_j + \langle \bm{v_{\textnormal{user $i$}}}, \bm{v_{\textnormal{item $j$}}} \rangle\]

\pause

With side information

\small \vspace{-3mm} \(y = \theta_i + e_j + \alert{w_{\textnormal{mobile}}} + \langle \bm{v_{\textnormal{user $i$}}}, \bm{v_{\textnormal{item $j$}}} \rangle + \langle \bm{v_{\textnormal{user $i$}}}, \alert{\bm{v_{\textnormal{mobile}}}} \rangle + \langle \bm{v_{\textnormal{item $j$}}}, \alert{\bm{v_{\textnormal{mobile}}}} \rangle\)

Graphically: logistic regression

\centering

Graphically: factorization machines

\centering

Formally: factorization machines

Each \textcolor{blue!80}{user}, \textcolor{orange}{item}, \textcolor{green!50!black}{skill} $k$ is modeled by bias $\alert{w_k}$ and embedding $\alert{\bm{v_k}}$.\vspace{2mm} \begin{columns} \begin{column}{0.47\linewidth} \includegraphics[width=\linewidth]{figures/fm.pdf} \end{column} \begin{column}{0.53\linewidth} \includegraphics[width=\linewidth]{figures/fm2.pdf} \end{column} \end{columns}\vspace{-2mm}

\hfill $\logit p(\bm{x}) = \mu + \underbrace{\sum_{k = 1}^N \alert{w_k} x_k}{\textnormal{logistic regression}} + \underbrace{\sum{1 \leq k < l \leq N} x_k x_l \langle \alert{\bm{v_k}}, \alert{\bm{v_l}} \rangle}_{\textnormal{pairwise relationships}}$

\small \fullcite{rendle2012factorization}

Training using MCMC

Priors: $w_k \sim \mathcal{N}(\mu_0, 1/\lambda_0) \quad \bm{v_k} \sim \mathcal{N}(\bm{\mu}, \bm{\Lambda}^{-1})$
Hyperpriors: $\mu_0, \ldots, \mu_n \sim \mathcal{N}(0, 1), \lambda_0, \ldots, \lambda_n \sim \Gamma(1, 1) = U(0, 1)$

\begin{algorithm}[H] \begin{algorithmic} \For {each iteration} \State Sample hyperp. $(\lambda_i, \mu_i)_i$ from posterior using Gibbs sampling \State Sample weights $\bm{w}$ \State Sample vectors $\bm{V}$ \State Sample predictions $\bm{y}$ \EndFor \end{algorithmic} \caption{MCMC implementation of FMs} \label{mcmc-fm} \end{algorithm}

Implementation in C++ (libFM) with Python wrapper (pyWFM).

\fullcite{rendle2012factorization}

Results

Datasets

\scriptsize

\input{tables/datasets}

Accuracy results on the Assistments dataset

\includegraphics{figures/assistments-results.pdf}

AUC results on the Assistments dataset

\centering \includegraphics[width=0.6\linewidth]{figures/barchart.pdf}

\scriptsize \input{tables/assistments42-full}

Bonus: interpreting the learned embeddings

\centering

\includegraphics{figures/viz.pdf}

Conclusion

Take home message

\alert{Knowledge tracing machines} unify many existing EDM models

It has better results than \alert{deep neural networks}

Do you have any questions?

Read our article:

\begin{block}{Knowledge Tracing Machines} \url{https://arxiv.org/abs/1811.03388} \end{block}

Try the code:

\centering \url{https://github.com/jilljenn/ktm}

\raggedright Feel free to chat (or tell me about your favorite manga or anime):

\centering vie@jill-jenn.net