Jill-Jênn Vie

Researcher at Inria

% Knowledge Tracing Machines:\newline Families of models\newline for predicting student performance % Jill-Jênn Vie \and Hisashi Kashima % November 9, 2018\bigskip\newline \url{https://arxiv.org/abs/1811.03388} — theme: Frankfurt handout: true institute: \includegraphics[height=1cm]{figures/aip-logo.png} \quad \includegraphics[height=1cm]{figures/kyoto.png} section-titles: false biblio-style: authoryear header-includes: - \usepackage{booktabs} - \usepackage{multicol} - \usepackage{bm} - \DeclareMathOperator\logit{logit} - \def\ReLU{\textnormal{ReLU}} biblatexoptions: - maxbibnames=99 - maxcitenames=5 —

Introduction

AI can:

recognize images
recognize speech
create fakes (generation)
play go (decision making)

as long as you have enough data.

Can it also:

\alert{improve education}

as long as you have enough data?

\pause

automatic exercise generation
\alert{prediction of student performance}
optimizing human learning

Predicting student performance

Data

A population of students answering questions

Events: “Student $i$ answered question $j$ correctly/incorrectly”

Goal

Learn the difficulty of questions automatically from data
Measure the knowledge of students
Potentially optimize their learning

Assumption

Good model for prediction $\rightarrow$ Good adaptive policy for teaching

Learning outcomes

\alert{Logistic regression} is amazing
- Unidimensional models of learning
- Takes IRT, PFA as special cases\vspace{1cm}
\alert{Factorization machines} are even more amazing
- Multidimensional models of learning
- Take MIRT as special case\vspace{1cm}
It makes sense to consider \alert{deep neural networks}
- What does deep knowledge tracing model exactly?

Families of models

Factorization Machines [@rendle2012factorization]
- Multidimensional Item Response Theory
- Logistic Regression
  - Item Response Theory (1980s)
  - Additive factor model (Cen, Hao, Koedinger, Junker, 2006)
  - Performance Factor Analysis (Pavlik, Cen, Koedinger, 2009)
Recurrent Neural Networks
- Deep Knowledge Tracing [@piech2015deep]

\vspace{5mm}

\fullcite{rendle2012factorization}

\fullcite{piech2015deep}

Problems

Weak generalization (in these slides)

Filling the blanks: some students did not attempt all questions

Strong generalization (in the paper)

Cold-start: some new students are not in the train set

Visually: model learning over time

\includegraphics[width=\linewidth]{figures/dkt.png}

\emph{From the DKT paper.}

Dummy dataset: weak generalization

\begin{columns} \begin{column}{0.6\linewidth} \begin{itemize} \item User 1 answered Item 1 correct \item User 1 answered Item 2 incorrect \item User 2 answered Item 1 incorrect \item User 2 answered Item 1 correct \item User 2 answered Item 2 ??? \end{itemize} \end{column} \begin{column}{0.4\linewidth} \centering \input{tables/dummy-ui-weak}\vspace{5mm}

\texttt{dummy.csv} \end{column} \end{columns}

Dummy dataset: strong generalization

\begin{columns} \begin{column}{0.6\linewidth} \begin{itemize} \item User 1 answered Item 1 correct \item User 1 answered Item 2 incorrect \item User 2 answered Item 1 ??? \item User 2 answered Item 1 ??? \item User 2 answered Item 2 ??? \end{itemize} \end{column} \begin{column}{0.4\linewidth} \centering \input{tables/dummy-ui-strong}\vspace{5mm}

\texttt{dummy.csv} \end{column} \end{columns}

Logistic Regression

Task 1: Item Response Theory

Learn abilities $\theta_i$ for each user $i$
Learn easiness $e_j$ for each item $j$ such that: $\begin{aligned} Pr(\textnormal{User $i$ Item $j$ OK}) & = \sigma(\theta_i + e_j)\\ \logit Pr(\textnormal{User $i$ Item $j$ OK}) & = \theta_i + e_j \end{aligned}$

Logistic regression

Learn $\alert{\bm{w}}$ such that $\logit Pr(\bm{x}) = \langle \alert{\bm{w}}, \bm{x} \rangle$

Usually with L2 regularization: ${

\bm{w}

}_2^2$ penalty $\leftrightarrow$ Gaussian prior

Graphically: IRT as logistic regression

Encoding of “User $i$ answered Item $j$”:

\centering

\[\logit Pr(\textnormal{User $i$ Item $j$ OK}) = \langle \bm{w}, \bm{x} \rangle = \theta_i + e_j\]

Encoding

python encode.py --users --items

\centering

\input{tables/show-ui}

data/dummy/X-ui.npz

\raggedright Then logistic regression can be run on the sparse features:

python lr.py data/dummy/X-ui.npz

Oh, there’s a problem

python encode.py --users --items

python lr.py data/dummy/X-ui.npz

\input{tables/pred-ui}

We predict the same thing when there are several attempts.

Count successes and failures

Keep track of what the student has done before:

\centering

\input{tables/dummy-uiswf}

data/dummy/data.csv

Task 2: Performance Factor Analysis

$W_{ik}$: how many successes of user $i$ over skill $k$ ($F_{ik}$: #failures)

Learn $\alert{\beta_k}$, $\alert{\gamma_k}$, $\alert{\delta_k}$ for each skill $k$ such that: $\logit Pr(\textnormal{User $i$ Item $j$ OK}) = \sum_{\textnormal{Skill } k \textnormal{ of Item } j} \alert{\beta_k} + W_{ik} \alert{\gamma_k} + F_{ik} \alert{\delta_k}$

python encode.py --skills --wins --fails

\centering \input{tables/show-swf}

data/dummy/X-swf.npz

Better!

python encode.py --skills --wins --fails

python lr.py data/dummy/X-swf.npz

\input{tables/pred-swf}

Test on a large dataset: Assistments 2009

278608 attempts of 4163 students over 196457 items on 124 skills.

Download http://jiji.cat/weasel2018/data.csv
Put it in data/assistments09

python fm.py data/assistments09/X-ui.npz (or make big)

\vspace{1cm}

\centering \input{tables/assistments42-afm-pfa}

Task 3: a new model (but still logistic regression)

python encode.py --items --skills --wins --fails

python lr.py data/dummy/X-iswf.npz

\centering \input{tables/assistments42-afm-pfa-iswf}

Factorization Machines

Here comes a new challenger

How to model \alert{side information} in, say, recommender systems?

Logistic Regression

Learn a 1-dim \alert{bias} for each feature (each user, item, etc.)

Factorization Machines

Learn a 1-dim \alert{bias} and a $k$-dim \alert{embedding} for each feature

What can be done with 2-dim embeddings?

\centering

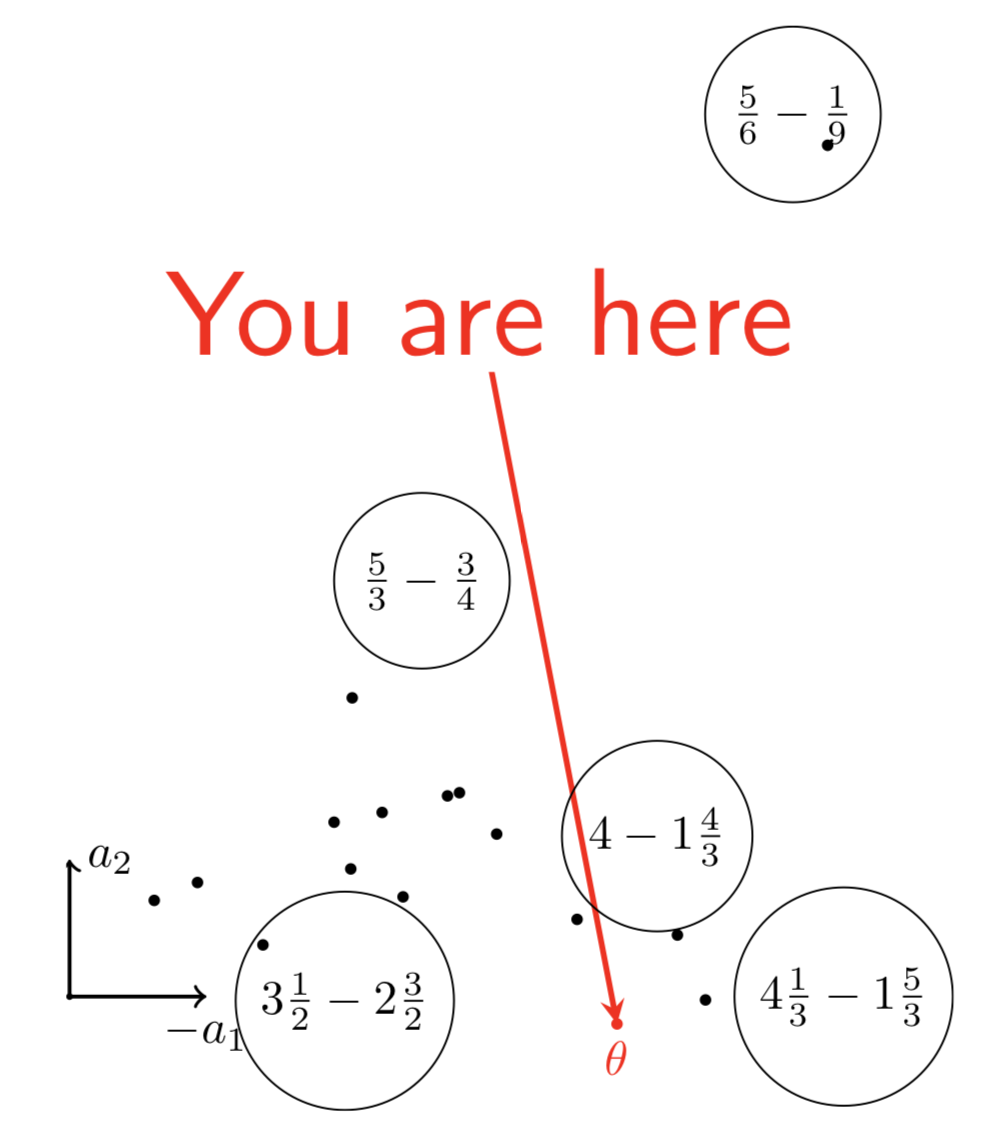{width=60%}

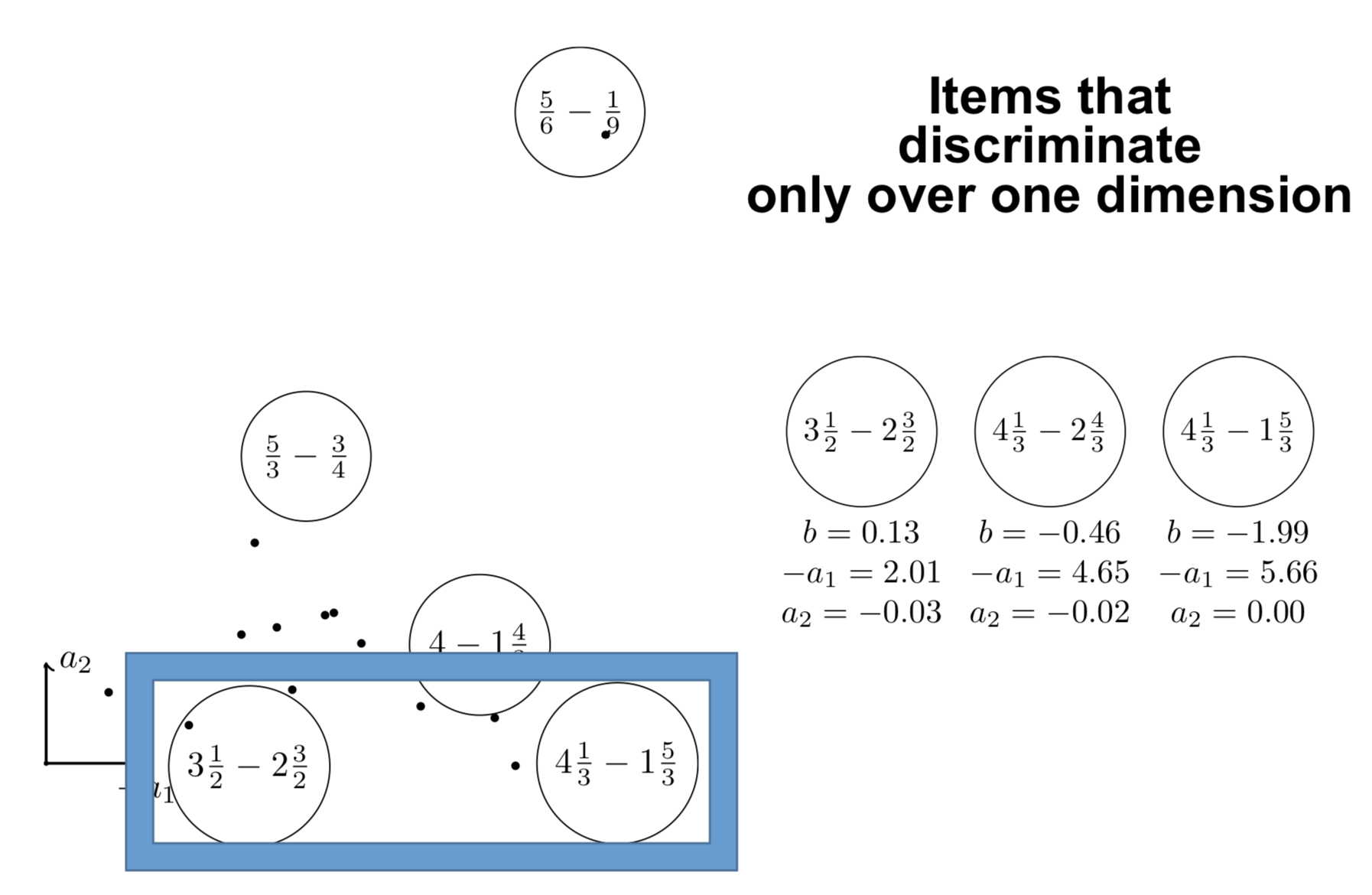
Interpreting the components

How to model side information?

If you know user $i$ attempted item $j$ on \alert{mobile} (not desktop)
How to model it?

$y$: score of event “user $i$ solves correctly item $j$”

IRT

\[y = \theta_i + e_j\]

Multidimensional IRT (similar to collaborative filtering)

\[y = \theta_i + e_j + \langle \bm{v_\textnormal{user $i$}}, \bm{v_\textnormal{item $j$}} \rangle\]

\pause

With side information

\[y = \theta_i + e_j + \langle \bm{v_\textnormal{user $i$}}, \bm{v_\textnormal{item $j$}} \rangle + \langle \bm{v_\textnormal{user $i$}}, \alert{\bm{v_\textnormal{mobile}}} \rangle + \langle \bm{v_\textnormal{item $j$}}, \alert{\bm{v_\textnormal{mobile}}} \rangle\]

Graphically: logistic regression

\centering

Graphically: factorization machines

\centering

Formally: factorization machines

Learn bias \alert{$w_k$} and embedding \alert{$\bm{v_k}$} for each feature $k$ such that: $\logit p(\bm{x}) = \mu + \underbrace{\sum_{k = 1}^N \alert{w_k} x_k}_{\textnormal{logistic regression}} + \underbrace{\sum_{1 \leq k < l \leq N} x_k x_l \langle \alert{\bm{v_k}}, \alert{\bm{v_l}} \rangle}_{\textnormal{pairwise interactions}}$

Multidimensional item response theory: $\logit p(\bm{x}) = \langle \bm{u_i}, \bm{v_j} \rangle + e_j$
is a particular case.

\small \fullcite{rendle2012factorization}

Deep Learning

Duolingo challenge: second language learning (2018)

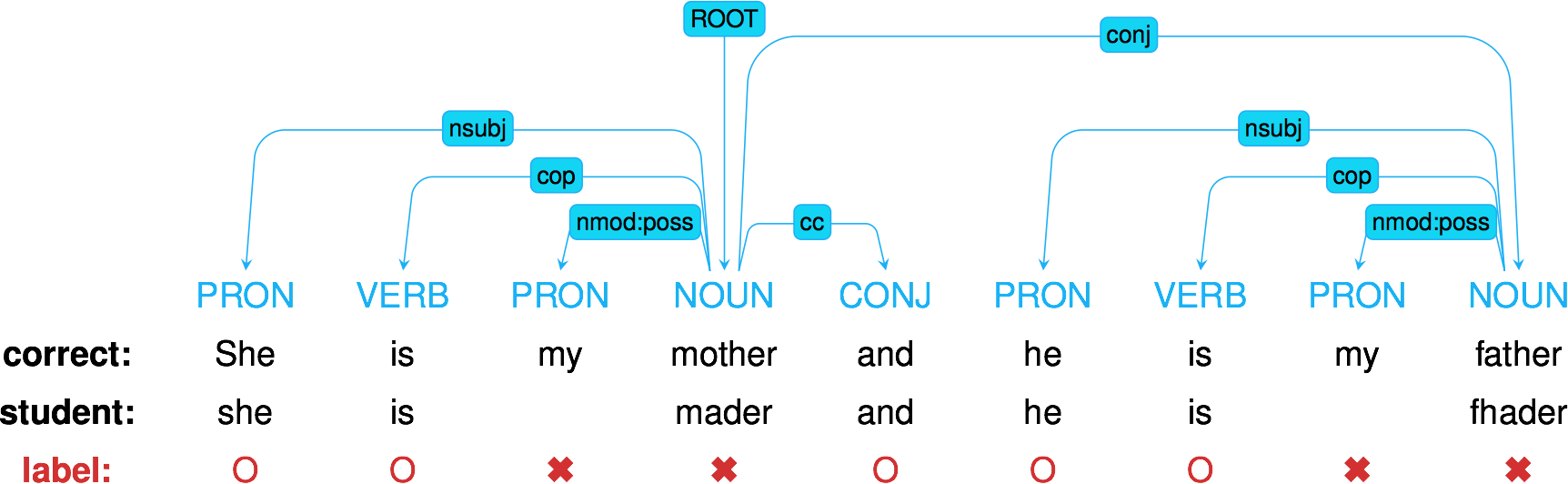
\centering \input{tables/duolingo}

Available on \url{http://sharedtask.duolingo.com}

Duolingo challenge: lots of side information!

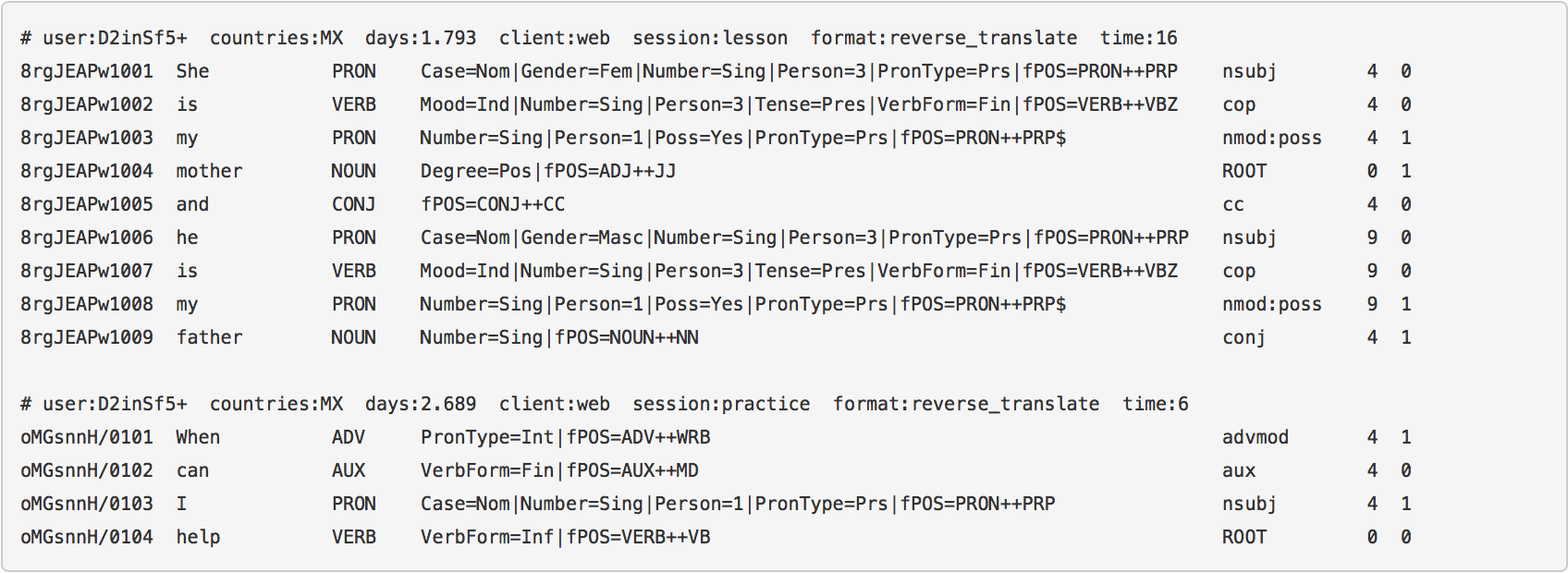
Deep Factorization Machines

Learn layers \alert{$W^{(\ell)}$} and \alert{$b^{(\ell)}$} such that: $\begin{aligned}[c] \bm{a}^{0}(\bm{x}) & = (\alert{\bm{v_{\texttt{user}}}}, \alert{\bm{v_{\texttt{item}}}}, \alert{\bm{v_{\texttt{skill}}}}, \ldots)\\ \bm{a}^{(\ell + 1)}(\bm{x}) & = \ReLU(\alert{W^{(\ell)}} \bm{a}^{(\ell)}(\bm{x}) + \alert{\bm{b}^{(\ell)}}) \quad \ell = 0, \ldots, L - 1\\ y_{DNN}(\bm{x}) & = \ReLU(\alert{W^{(L)}} \bm{a}^{(L)}(\bm{x}) + \alert{\bm{b}^{(L)}}) \end{aligned}$

\[\logit p(\bm{x}) = y_{FM}(\bm{x}) + y_{DNN}(\bm{x})\]

\small \fullcite{Duolingo2018}

Duolingo ranking

\centering

\begin{tabular}{cccc} \toprule Rank & Team & Algo & AUC\ \midrule 1 & SanaLabs & RNN + GBDT & .857
2 & singsound & RNN & .854
2 & NYU & GBDT & .854
4 & CECL & LR + L1 (13M feat.) & .843
5 & TMU & RNN & .839\ \midrule (7) & JJV & KTM == FM & .822
(8) & JJV & DeepFM & .814
10 & JJV & DeepFM & .809\ \midrule – & JJV & KTM == LR + L2 & .783
15 & Duolingo & LR + L1 & .771\ \bottomrule \end{tabular}

\raggedright \small \fullcite{Settles2018}

What ‘bout recurrent neural networks?

Deep Knowledge Tracing: model the problem as sequence prediction

Each student on skill $q_t$ has performance $a_t$
How to predict outcomes $\bm{y}$ on every skill $k$?
Spoiler: by measuring the evolution of a latent state $\alert{\bm{h_t}}$

Graphically: deep knowledge tracing

\centering

Graphically: there is a MIRT in my DKT

\centering

Drawback of Deep Knowledge Tracing

DKT does not model individual differences.

Actually, Wilson even managed to beat DKT with (1-dim!) IRT.

By estimating on-the-fly the student’s learning ability, we managed to get a better model.

\centering \input{tables/results-dkt}

\raggedright \small \fullcite{Minn2018}

Results

\input{tables/assistments42-full}

Conclusion

Take home message

\alert{Factorization machines} are a strong baseline that unifies many existing EDM models

It is better to estimate an item per bias, not only per skill
Side information improves performance more than higher $d$

\alert{Recurrent neural networks} are powerful because they track the evolution of the latent state

Most existing models (like DKT) cannot handle multiple skills, but KTM do
We should combine DKT with side information

\fullcite{KTM2018}

Any suggestions are welcome!

Read our article:

\begin{block}{Knowledge Tracing Machines} \url{https://arxiv.org/abs/1811.03388} \end{block}

Try the code:

\centering \url{https://github.com/jilljenn/ktm}

\raggedright Feel free to chat:

\centering vie@jill-jenn.net

\raggedright Do you have any questions?

Jill-Jênn Vie

Researcher at Inria

Introduction

AI for Social Good

Predicting student performance

Data

Goal

Assumption

Learning outcomes

Families of models

Problems

Weak generalization (in these slides)

Strong generalization (in the paper)

Visually: model learning over time

Dummy dataset: weak generalization

Dummy dataset: strong generalization

Logistic Regression

Task 1: Item Response Theory

Logistic regression

Graphically: IRT as logistic regression

Encoding

Oh, there’s a problem

Count successes and failures

Task 2: Performance Factor Analysis

Better!

Test on a large dataset: Assistments 2009

Task 3: a new model (but still logistic regression)

Factorization Machines

Here comes a new challenger

Logistic Regression

Factorization Machines

What can be done with 2-dim embeddings?

Interpreting the components

Interpreting the components

How to model side information?

IRT

Multidimensional IRT (similar to collaborative filtering)

With side information

Graphically: logistic regression

Graphically: factorization machines

Formally: factorization machines

Deep Learning

Duolingo challenge: second language learning (2018)

Duolingo challenge: lots of side information!

Deep Factorization Machines

Duolingo ranking

What ‘bout recurrent neural networks?

Graphically: deep knowledge tracing

Graphically: there is a MIRT in my DKT

Drawback of Deep Knowledge Tracing

Results

Conclusion

Take home message

Any suggestions are welcome!