Jill-Jênn Vie
Researcher at Inria
% Using Ratings & Posters\newline for Anime & Manga Recommendations % Jill-Jênn Vie % August 31, 2017 — header-includes: - \usepackage{tikz} - \usepackage{array} - \usepackage{icomma} - \usepackage{multicol,booktabs} - \def\R{\mathcal{R}} handout: true —
Recommendation System
Problem
- Every user rates few items (1 %)
- How to infer missing ratings?
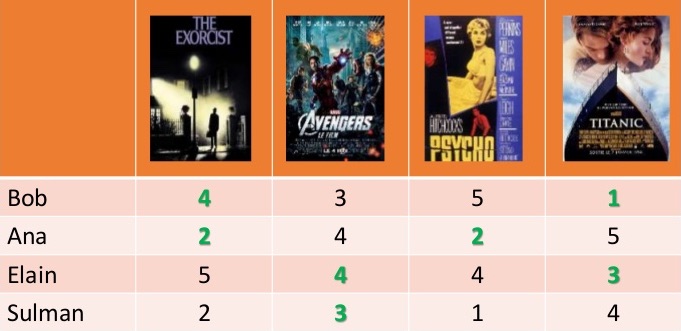 \
\
Every supervised machine learning algorithm
fit($X$, $y$)
\centering
\begin{tabular}{ccc} \toprule
\multicolumn{2}{c}{$X$} & $y$\ \cmidrule{1-2}
\texttt{user_id} & \texttt{work_id} & \texttt{rating}\ \midrule
24 & 823 & like
12 & 823 & dislike
12 & 25 & favorite
\ldots & \ldots & \ldots\ \bottomrule
\end{tabular}
\pause
$\hat{y}$ = predict($X$)
\centering
\begin{tabular}{ccc} \toprule
\multicolumn{2}{c}{$X$} & $\hat{y}$\ \cmidrule{1-2}
\texttt{user_id} & \texttt{work_id} & \texttt{rating}\ \midrule
24 & 25 & \only<2>{?}\only<3>{\alert{disliked}}
12 & 42 & \only<2>{?}\only<3>{\alert{liked}}\ \bottomrule
\end{tabular}
Evaluation: Root Mean Squared Error (RMSE)
If I predict $\hat{y_i}$ for each user-work pair to test among $n$,
while truth is $y^*_i$:
Dataset 1: Movielens
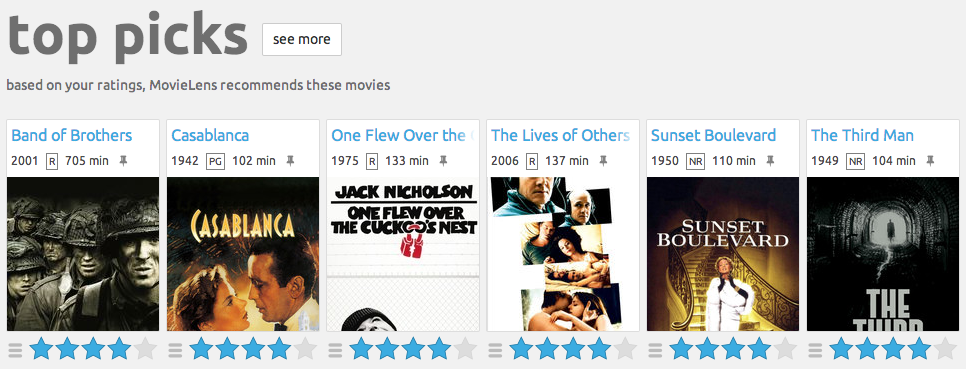 \
\
- 700 users
- 9000 movies
- 100000 ratings
Dataset 2: Mangaki
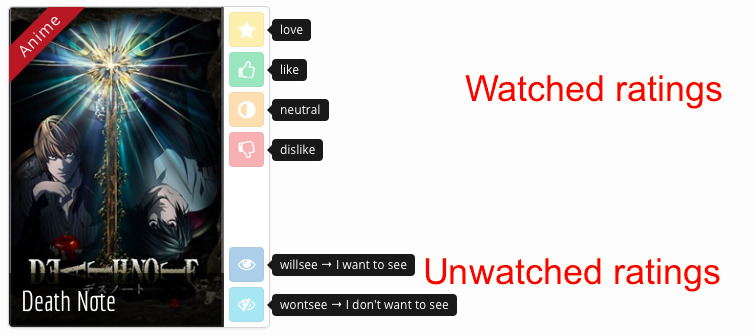 \
\
- 2100 users
- 15000 works \textcolor{gray}{\hfill {\em \small anime / manga / OST}}
- 310000 ratings \textcolor{gray}{\hfill {\em \small fav / like / dislike / neutral / willsee / wontsee}}
- User can rate anime or manga
- And receive recommendations
- Also reorder their watchlist
\pause
- Code is 100% on GitHub
- Awards from Microsoft and Kokusai Kōryū Kikin
- Ongoing data challenge on universityofbigdata.net
KNN $\rightarrow$ measure similarity
$K$-nearest neighbors
- $\R_u$ represents the row vector of user $u$ in the rating matrix (users $\times$ works).
- Similarity score between users (cosine): \(score(u, v) = \frac{\R_u \cdot \R_v}{||\R_u|| \cdot ||\R_v||}.\)
- Let’s identify the $k$-nearest neighbors of user $u$
- And recommend to user $u$ what $u$’s neighbors liked
but $u$ didn’t see
Hint
| If $R’$ the $N \times M$ matrix of rows $\frac{\R_u}{ | \R_u | }$, we can get the $N \times N$ score matrix by computing $R’ R’^T$. |
PCA, SVD $\rightarrow$ reduce dimension to generalize
Matrix factorization
\vspace{-7mm}
\(R = \left(\begin{array}{c} \R_1\\ \R_2\\ \vdots\\ \R_n \end{array}\right) = \raisebox{-1cm}{\begin{tikzpicture} \draw (0,0) rectangle (2.5,2); \end{tikzpicture}} = \raisebox{-1cm}{\begin{tikzpicture} \draw (0,0) rectangle ++(1,2); \draw node at (0.5,1) {$C$}; \draw (1.1,1) rectangle ++(2.5,1); \draw node at (2.35,1.5) {$P$}; \end{tikzpicture}}\) Each row $\R_u$ is a linear combination of profiles $P$.
\pause
Interpreting Key Profiles
\begin{tabular}{@{}lccc@{}}
If $P$ & $P_1$: adventure & $P_2$: romance & $P_3$: plot twist
And $C_u$ & $0,2$ & $-0,5$ & $0,6$
\end{tabular}
$\Rightarrow$ $u$ \alert{likes a bit} adventure, \alert{hates} romance, \alert{loves} plot twists.
\vspace{2mm}
\pause
Singular Value Decomposition
$R = (U \cdot \Sigma)V^T$ where $U : N \times r$ et $V : M \times r$ are orthogonal and $\Sigma : r \times r$ is diagonal.
Visualizing first two columns of $V_j$ in SVD
\alert{Closer} points mean similar taste
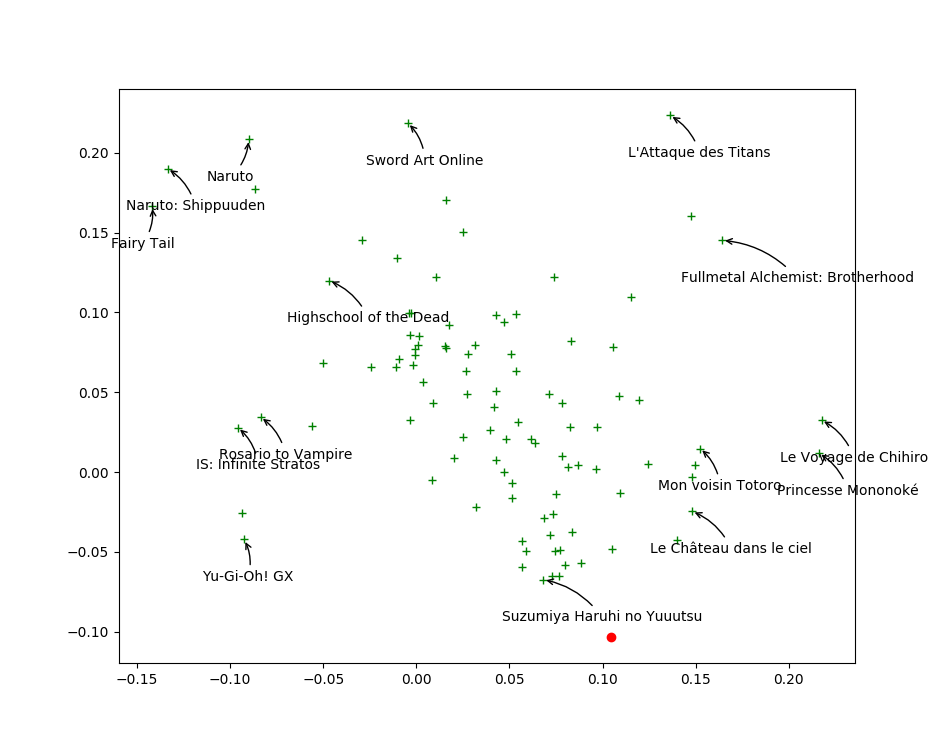 \
\
Find your taste by plotting first two columns of $U_i$
You will \alert{like} movies that are \alert{close to you}
 \
\
Variants of Matrix Factorization
$R$ ratings, $C$ coefficients, $P$ profiles ($F$ features).
$R = CP = CF^T \Rightarrow r_{ij} \simeq \hat{r}_{ij} \triangleq C_i \cdot F_j$.
Objective functions (reconstruction error) to minimize
SVD : $\sum_{i, j}~(r_{ij} - C_i \cdot F_j)^2$ (deterministic)
\pause
ALS : $\sum_{i, j \textnormal{\alert{ known}}}~(r_{ij} - C_i \cdot F_j)^2$
\pause
| ALS-WR : $\sum_{i, j \textnormal{\alert{ known}}}~(r_{ij} - C_i \cdot F_j)^2 + \lambda (\sum_i N_i | C_i | ^2 + \sum_j M_j | F_j | ^2)$ |
\pause
| WALS by Tensorflow™ : $$\sum_{i, j} w_{ij} \cdot (r_{ij} - C_i \cdot F_j)^2 + \lambda (\sum_i | C_i | ^2 + \sum_j | F_j | ^2)$$ |
\pause
Who do you think wins?
About the Netflix Prize
- On October 2, 2006, Netflix organized an online contest:
The first one who beats our algorithm (Cinematch) by more than 10% will receive 1,000,000 USD.
and gave anonymized data- Half of world AI community suddenly became interested
in this problem- October 8, someone beat Cinematch
- October 15, 3 teams beat it, notably by 1.06%
- June 26, 2009, team 1 beat Cinematch by 10.05%
$\rightarrow$ \alert{last call}: still one month to win- July 25, 2009, \alert{team 2} beat Cinematch by 10.09%
- Team 1 does 10.09% also
- 20 minutes later \alert{team 2} does 10.10%
- … Actually, both teams were ex \ae quo on the validation set
- … So the first team to send their results won (team 1, 10.09%)
Privacy concerns
- August 2009, Netflix wanted to restart a contest
- Meanwhile, in 2007 two researchers from Texas University could \alert{de-anonymize} users by crossing data with IMDb
- (approximate birth year, zip code, watched movies)
- In December 2009, 4 Netflix users sued Netflix
- March 2010, amicable settlement (enmankaiketsu)
$\rightarrow$ complaint is closed
ALS for feature extraction
$R = CP$
Issue: Item Cold-Start
- If no ratings are available for an anime
$\Rightarrow$ no feature will be trained - If anime features at put to 0
$\Rightarrow$ prediction of ALS will be constant for every unrated anime.
\pause
But we have posters!
- On Mangaki, almost all works have a poster
- How to extract information?
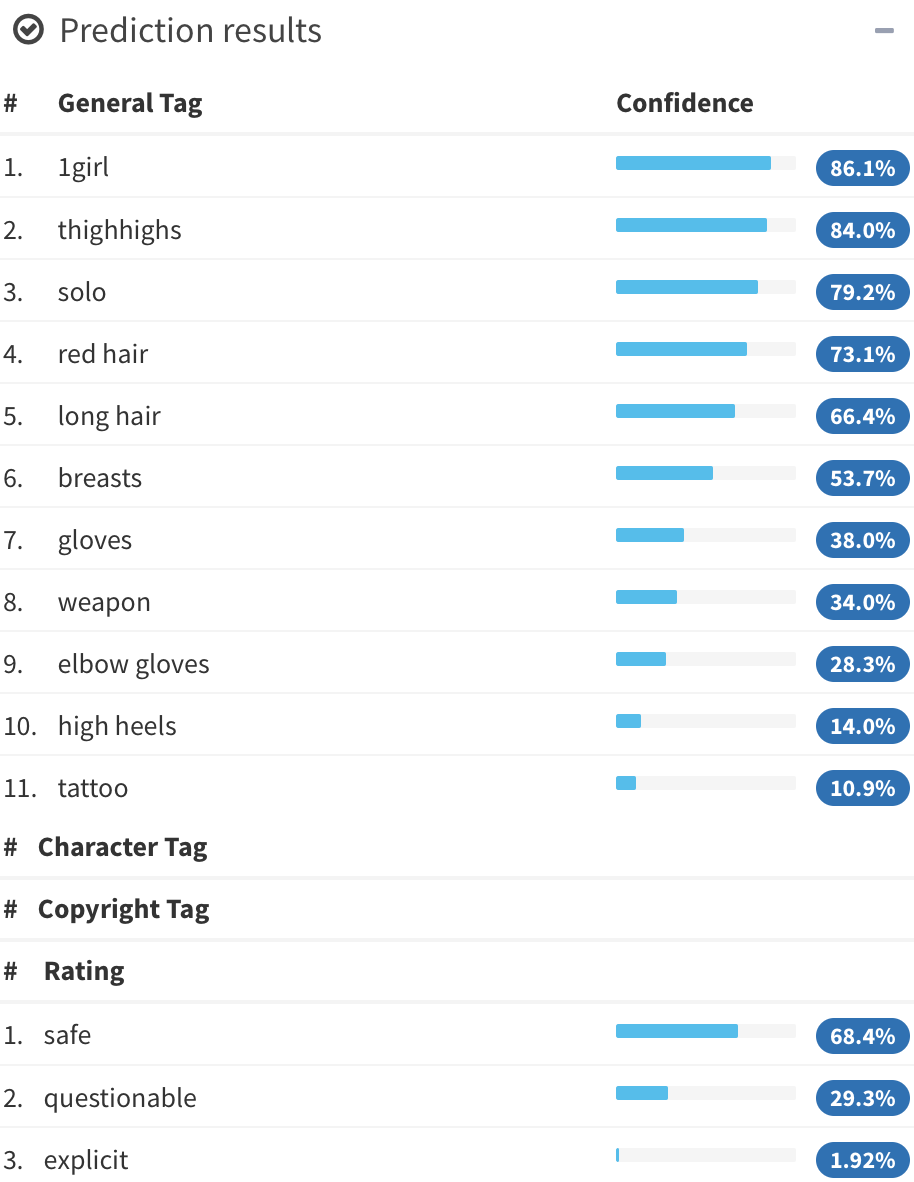
Illustration2Vec (Saito and Matsui, 2015)
\centering
 {width=40%}\
{width=40%}\
 {width=40%}\
{width=40%}\
- CNN pretrained on ImageNet, trained on Danbooru
(1.5M illustrations with tags) - 502 most frequent tags kept, outputs \alert{tag weights}
LASSO for explanation of user preferences
$T$ matrix of 15000 works $\times$ 502 tags
- Each user is described by its preferences $P$
$\rightarrow$ a \alert{sparse} row of weights over tags. - Estimate user preferences $P$ such that $r_{ij} \simeq PT^T$.
Interpretation and explanation
- You seem to like \alert{\emph{magical girls}} but not \alert{\emph{blonde hair}}
$\Rightarrow$ Look! All of them are \alert{\emph{brown hair}}! Buy now!
Least Absolute Shrinkage and Selection Operator (LASSO)
\[\frac1{2 N_i} {\lVert \R_i - P_i T^T \rVert}_2^2 + \alpha \alert{ {\lVert P_i \rVert}_1}.\]\noindent where $N_i$ is the number of items rated by user $i$.
Blending
We would like to do:
\[\hat{r}_{ij}^{BALSE} = \begin{cases} \hat{r}_{ij}^{ALS} & \text{if item $j$ was rated at least $\gamma$ times}\\ \hat{r}_{ij}^{LASSO} & \text{otherwise} \end{cases}\]But we can’t. Why?
\pause
\[\hat{r}_{ij}^{BALSE} = \alert{\sigma(\beta(R_j - \gamma))} \hat{r}_{ij}^{ALS} + \left(1 - \alert{\sigma(\beta(R_j - \gamma))}\right) \hat{r}_{ij}^{LASSO}\]\noindent
where $R_j$ denotes the number of ratings of item $j$
$\beta$ and $\gamma$ are learned by stochastic gradient descent.
\pause
\centering
We call this gate the \alert{Steins;Gate}.
Blended Alternate Least Squares with Explanation
\centering
\
\pause
We call this model \alert{BALSE}.
Results
\centering
\
Thank you!
\centering
 {width=50%}\
{width=50%}\
\raggedright
Read this article
http://jiji.cat/bigdata/balse.pdf (soon on arXiv)
Compete to Mangaki Data Challenge
research.mangaki.fr (problem + University of Big Data)
Reproduce our results on GitHub
github.com/mangaki