Jill-Jênn Vie

Researcher at Inria

% Algorithmes de recommandation :\newline comment ça marche ? \vspace{-5mm} % \vspace{-5mm} {height=3.1cm} Florian {height=3.1cm} Ryan {height=3.1cm} Hisashi {height=3.1cm}\newline \alert{Jill-Jênn Vie}¹³; Solène Pichereau³; Ryan Lahfa³; Hisashi Kashima²\newline; Basile Clement³; Kévin Cocchi³; Thomas Chalumeau³; Florian Yger\textsuperscript4 % ¹ Inria\newline ² Université de Kyoto \& RIKEN AIP (Tokyo)\newline ³ Mangaki (Paris, France)\newline \textsuperscript4 Université Paris-Dauphine \hfill \raisebox{-1em}{\includegraphics[width=2cm]{figures/mangakiwhite.png}} — theme: metropolis lang: french babel-lang: french header-includes: - \usepackage{tikz} - \usepackage{array} - \usepackage{icomma} - \usepackage{multicol,booktabs} - \def\R{\mathcal{R}} - \usecolortheme{owl} - \def\no{n\textsuperscript{o}} section-titles: false —

Recommandation d’articles

\includegraphics[width=\linewidth]{figures/amazon.jpg}

Mangaki, recommandations d’anime/manga

Notez des anime/manga et recevez des recommandations

380 000 notes de 8 000 utilisateurs sur 29 000 œuvres

Codé en Python

Tout le code est libre et ouvert : \alert{github.com/mangaki}

Prix : Microsoft Prize (2014) Japan Foundation (2016)

Financé par NLnet (Pays-Bas), Commission européenne

Systèmes de recommandation

Problem

Chaque personne note peu d’œuvres (1 %)
Comment inférer les notes manquantes ?

Example

\begin{tabular}{ccccc} & \includegraphics[height=2.5cm]{figures/1.jpg} & \includegraphics[height=2.5cm]{figures/2.jpg} & \includegraphics[height=2.5cm]{figures/3.jpg} & \includegraphics[height=2.5cm]{figures/4.jpg}
Sacha & ? & 5 & 2 & ?
Ondine & 4 & 1 & ? & 5
Pierre & 3 & 3 & 1 & 4
Joëlle & 5 & ? & 2 & ? \end{tabular}

Systèmes de recommandation

Problem

Chaque personne note peu d’œuvres (1 %)
Comment inférer les notes manquantes ?

Example

\begin{tabular}{ccccc} & \includegraphics[height=2.5cm]{figures/1.jpg} & \includegraphics[height=2.5cm]{figures/2.jpg} & \includegraphics[height=2.5cm]{figures/3.jpg} & \includegraphics[height=2.5cm]{figures/4.jpg}
Sacha & \alert{3} & 5 & 2 & \alert{2}
Ondine & 4 & 1 & \alert{4} & 5
Pierre & 3 & 3 & 1 & 4
Joëlle & 5 & \alert{2} & 2 & \alert{5} \end{tabular}

Qu’est-ce qu’un algorithme de machine learning ?

Fit (entraîner)

\def\Zootopia{\emph{Zootopie}} \def\Porco{\emph{Porco Rosso}} \def\Tokikake{\emph{La Traversée du temps}} \def\Martian{\emph{Seul sur Mars}}

\begin{center} \begin{tabular}{rcl} \toprule Ondine & \alert{aime} & \Zootopia
Ondine & \alert{adore} & \Porco
Sacha & \alert{adore} & \Tokikake
Sacha & \alert{n’aime pas} & \Martian\ \bottomrule \end{tabular} \end{center}

Predict (prédire)

\begin{center} \begin{tabular}{rcl} \toprule Ondine & \alert{\only<1>{?}\only<2>{adore}} & \Martian
Sacha & \alert{\only<1>{?}\only<2>{aime}} & \Zootopia\ \bottomrule \end{tabular} \end{center}

Qu’est-ce qu’un \alert{mauvais} algorithme de machine learning ?

Fit

\begin{center} \begin{tabular}{rcl} \toprule Ondine & \alert{like} & \Zootopia
Ondine & \alert{favorite} & \Porco
Sacha & \alert{favorite} & \Tokikake
Sacha & \alert{dislike} & \Martian\ \bottomrule \end{tabular} \end{center}

\hfill 100 % correct

Predict

\begin{center} \begin{tabular}{rcl} \toprule Ondine & \alert{n’aime pas} & \Martian{} (en fait : adore)
Sacha & \alert{neutre} & \Zootopia{} (en fait : aime)\ \bottomrule \end{tabular} \end{center}

\hfill 20 % correct

N’arrive pas à \alert{généraliser}

Qu’est-ce qu’un \alert{bon} algorithme de machine learning ?

Fit

\begin{center} \begin{tabular}{rcl} \toprule Ondine & \alert{adore} & \Zootopia{} (en fait : aime)
Ondine & \alert{adore} & \Porco
Sacha & \alert{adore} & \Tokikake
Sacha & \alert{n’aime pas} & \Martian\ \bottomrule \end{tabular} \end{center}

\hfill 90 % correct

Predict

\begin{center} \begin{tabular}{rcl} \toprule Ondine & \alert{aime} & \Martian{} (en fait : adore)
Sacha & \alert{adore} & \Zootopia{} (en fait : aime)\ \bottomrule \end{tabular} \end{center}

\hfill 90 % correct

Comment comparer des méthodes ?

\centering \begin{tabular}{cccccc} n’aime pas & ne verra pas & neutre & veut voir & aime & adore
-2 & -0.5 & 0.1 & 0.5 & 2 & 4 \end{tabular}

\raggedright

Pénalités

Si je prédis :: \alert{adore} pour adore $\rightarrow$ erreur de 0
\alert{n’aime pas} pour adore $\rightarrow$ erreur de $(4 - (-2))^2 = 36$
\alert{aime} for adore $\rightarrow$ erreur de 4

Erreur : moyenne des (différences)²
RMSE : racine carrée de la valeur ci-dessus

\alert{Validation croisée}

On entraîne sur 80 % des données (entraînement)
On cache les 20 % de données restantes (validation)
On s’en sert pour évaluer la performance des modèles

Plus l’erreur de validation est basse, mieux c’est

Algorithme des plus proches voisins

Pour recommander des films à quelqu’un :

On introduit un \alert{score de similarité} entre personnes
On détermine les 10 personnes \alert{les plus proches} de quelqu’un
On lui recommande ce qu’elles ont aimé qu’il n’a pas vu

Nos données

\begin{tabular}{c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c} & \footnotesize{007} & \footnotesize{Batman 1} & \footnotesize{Shrek 2} & \footnotesize{Toy Story 3} & \footnotesize{Star Wars 4} & \footnotesize{Twilight 5}
Alice & $+$ & $-$ & $0$ & $+$ & $0$ & $-$
Bob & $-$ & $0$ & $+$ & $-$ & $+$ & $+$
Charles & $+$ & $+$ & $+$ & $+$ & $-$ & $-$
Daisy & $+$ & $+$ & $0$ & $0$ & $+$ & $-$
Everett & $+$ & $-$ & $+$ & $+$ & $-$ & $0$
\end{tabular}

\begin{center} Quel score de similarité entre utilisateurs choisir ? \end{center}

Calcul du score

\centering

À quel point Alice est proche de Charles ?

Calcul du score

\begin{tabular}{c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c} & \footnotesize{007} & \footnotesize{Batman 1} & \footnotesize{Shrek 2} & \footnotesize{Toy Story 3} & \footnotesize{Star Wars 4} & \footnotesize{Twilight 5}
Alice & $+$ & $-$ & $0$ & $+$ & $0$ & $-$
Charles & $+$ & $+$ & $+$ & $+$ & $-$ & $-$
Score & $+1$ & $-1$ & & $+1$ & & +1
\end{tabular} \vspace{-1mm} \begin{center} $score(\textnormal{Alice}, \textnormal{Charles}) = 3 + (-1) = \alert{2}$
\end{center} \vspace{2mm}

\begin{tabular}{c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c} & \footnotesize{007} & \footnotesize{Batman 1} & \footnotesize{Shrek 2} & \footnotesize{Toy Story 3} & \footnotesize{Star Wars 4} & \footnotesize{Twilight 5}
Alice & $+$ & $-$ & $0$ & $+$ & $0$ & $-$
Bob & $-$ & $0$ & $+$ & $-$ & $+$ & $+$
Score & $-1$ & & & $-1$ & & -1
\end{tabular} \vspace{-1mm} \begin{center} $score(\textnormal{Alice}, \textnormal{Bob}) = \alert{-3}$\bigskip \vspace{2mm}

Alice est \alert{plus proche} de Charles que de Bob \end{center}

Score de similarité entre personnes

\begin{center} \begin{tabular}{c@{\hspace{2mm}}|c@{\hspace{2mm}}c@{\hspace{2mm}}c@{\hspace{2mm}}c@{\hspace{2mm}}c} & Alice & Bob & Charles & Daisy & Everett
\hline Alice & $4$ & $-3$ & $2$ & $1$ & $3$
Bob & $-3$ & $5$ & $-3$ & $-1$ & $-2$
Charles & $2$ & $-3$ & $6$ & $2$ & $3$
Daisy & $1$ & $-1$ & $2$ & $4$ & $-1$
Everett & $3$ & $-2$ & $3$ & $-1$ & $5$
\end{tabular} \end{center}

\begin{center} Qui sont les 2 plus proches voisins d’Alice ? \end{center}

Calcul des prédictions

\begin{tabular}{c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c} & \footnotesize{007} & \footnotesize{Batman 1} & \footnotesize{Shrek 2} & \footnotesize{Toy Story 3} & \footnotesize{Star Wars 4} & \footnotesize{Twilight 5}
Alice & $+$ & $-$ & \alert{?} & $+$ & \alert{?} & $-$
Charles & $+$ & $+$ & $+$ & $+$ & $-$ & $-$
Daisy & $+$ & $+$ & $0$ & $0$ & $+$ & $-$
Everett & $+$ & $-$ & $+$ & $+$ & $-$ & $0$
\end{tabular}

\begin{center} Connaissant ses voisin$\cdot$es, quelles sont les chances d’Alice d’apprécier ces films ? \end{center}

Calcul des prédictions

\begin{tabular}{c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c@{\hspace{3mm}}c} & \footnotesize{007} & \footnotesize{Batman 1} & \footnotesize{Shrek 2} & \footnotesize{Toy Story 3} & \footnotesize{Star Wars 4} & \footnotesize{Twilight 5}
Alice & $+$ & $-$ & \alert{$+$} & $+$ & \alert{$-$} & $-$
Charles & $+$ & $+$ & $+$ & $+$ & $-$ & $-$
Daisy & $+$ & $+$ & $0$ & $0$ & $+$ & $-$
Everett & $+$ & $-$ & $+$ & $+$ & $-$ & $0$
\end{tabular}

\begin{center} On peut calculer la moyenne :
$prediction(\textnormal{Alice}, \textnormal{Star Wars 4}) = -0,333$… \end{center}

Factorisation de matrice $\rightarrow$ réduire la dimension pour généraliser

Idée : Apprendre une représentation des utilisateurs et œuvres
de sorte que les gens aiment des œuvres proches d’eux

Fit

$R$ notes, \alert{$U$} vecteurs des utilisateurs, \alert{$W$} vecteurs des œuvres.

\[R = \alert{UW^T} \qquad \hat{r}_{ij}^{ALS} = \langle U_i, W_j \rangle\]

\pause

Predict : Est-ce que l’utilisateur $i$ va aimer l’œuvre $j$?

Il suffit de calculer $\langle \alert{U_i}, \alert{W_j} \rangle$ pour le savoir

Algorithme \alert{ALS} : moindres carrés alternés (Zhou, 2008)

Jusqu’à convergence (~ 20 itérations) :
- Fixer $U$ (utilisateurs) améliorer $W$ (œuvres)
  \hfill de façon à minimiser l’erreur
- Fixer $W$ améliorer $U$

Illustration de la minimisation alternée

\only<1>{\includegraphics{figures/embed0.pdf}} \only<2>{\includegraphics{figures/embed1.pdf}} \only<3>{\includegraphics{figures/embed2.pdf}} \only<4>{\includegraphics{figures/embed3.pdf}} \only<5>{\includegraphics{figures/embed4.pdf}} \only<6>{\includegraphics{figures/embed5.pdf}} \only<7>{\includegraphics{figures/embed6.pdf}} \only<8>{\includegraphics{figures/embed7.pdf}} \only<9>{\includegraphics{figures/embed8.pdf}} \only<10>{\includegraphics{figures/embed9.pdf}} \only<11>{\includegraphics{figures/embed10.pdf}} \only<12>{\includegraphics{figures/embed11.pdf}} \only<13>{\includegraphics{figures/embed12.pdf}} \only<14>{\includegraphics{figures/embed13.pdf}} \only<15>{\includegraphics{figures/embed14.pdf}} \only<16>{\includegraphics{figures/embed15.pdf}} \only<17>{\includegraphics{figures/embed16.pdf}} \only<18>{\includegraphics{figures/embed17.pdf}} \only<19>{\includegraphics{figures/embed18.pdf}} \only<20>{\includegraphics{figures/embed19.pdf}} \only<21>{\includegraphics{figures/embed20.pdf}} \only<22>{\includegraphics{figures/embed21.pdf}} \only<23>{\includegraphics{figures/embed22.pdf}} \only<24>{\includegraphics{figures/embed23.pdf}} \only<25>{\includegraphics{figures/embed24.pdf}} \only<26>{\includegraphics{figures/embed25.pdf}} \only<27>{\includegraphics{figures/embed26.pdf}} \only<28>{\includegraphics{figures/embed27.pdf}} \only<29>{\includegraphics{figures/embed28.pdf}} \only<30>{\includegraphics{figures/embed29.pdf}} \only<31>{\includegraphics{figures/embed30.pdf}} \only<32>{\includegraphics{figures/embed31.pdf}} \only<33>{\includegraphics{figures/embed32.pdf}} \only<34>{\includegraphics{figures/embed33.pdf}} \only<35>{\includegraphics{figures/embed34.pdf}} \only<36>{\includegraphics{figures/embed35.pdf}} \only<37>{\includegraphics{figures/embed36.pdf}} \only<38>{\includegraphics{figures/embed37.pdf}} \only<39>{\includegraphics{figures/embed38.pdf}}

Visualisation des œuvres : points proches $\iff$ goûts similaires

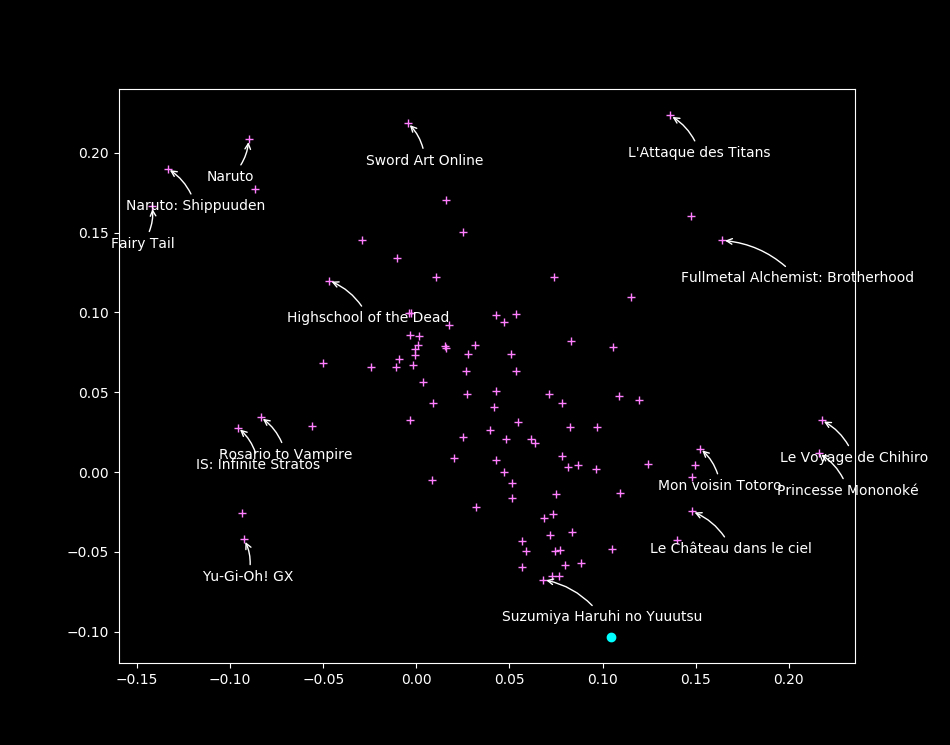Où êtes-vous sur la carte ?

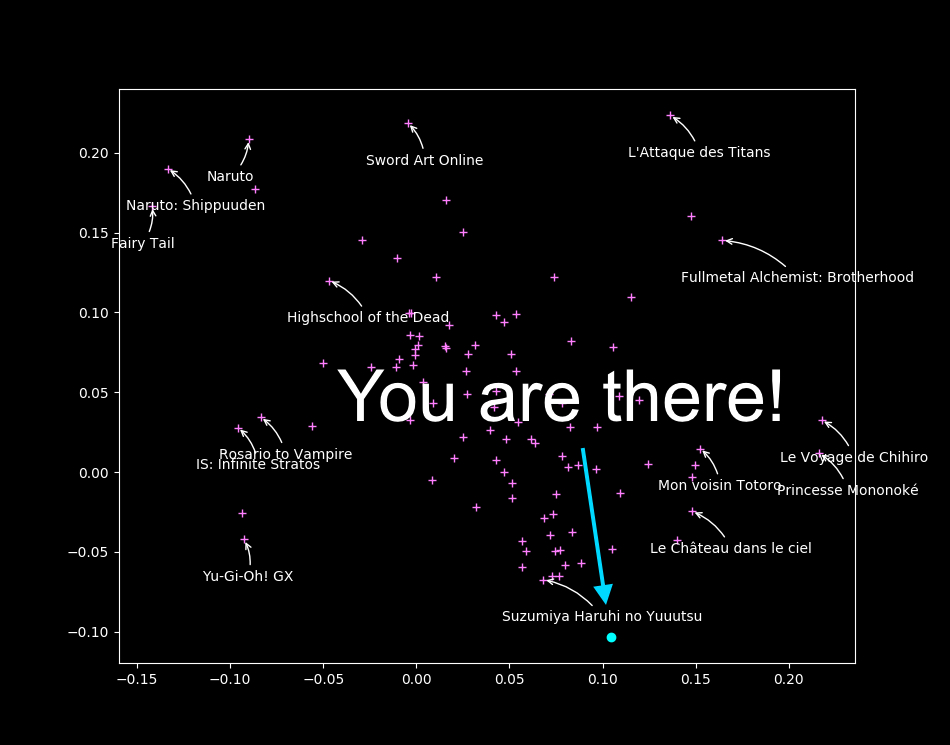Mangaki Map: \alert{\href{https://mangaki.fr/map}{mangaki.fr/map}}

Est-ce la méthode parfaite ?

À votre avis ?

\pause

Problème : démarrage à froid

Si on n’a pas de notes pour une œuvre
on ne sait pas où elle est sur la carte :-(

Aucun moyen de distinguer entre œuvres non notées

Mais on a énormément de posters !

Comment utiliser cette information pour améliorer les recommandations ?

Illustration2Vec (Saito and Matsui, 2015)

\centering

{height=70%}\ {height=70%}\

\small (Solène Pichereau, sedeto.fr) \qquad (Saito and Matsui, 2015)

\normalsize

Modèle CNN entraîné sur des photos (ImageNet, Danbooru)
Reconnaît 502 tags, pondérés par confiance

Représentation des œuvres et des posters

{width=48%} {width=48%}

Posters proches

Étape suivante ?

Extraire les frames des épisodes

\hfill \emph{Cowboy Bebop EP 23} “Brain Scratch”, Sunrise

Bientôt : assistant de visionnage

Quels sont les risques ?

Une petite anecdote

Le 2 octobre 2006, Netflix a lancé un concours :
Le premier qui bat notre algorithme de plus de 10 % remportera 1 million de dollars.
et ont filé des données pseudononymisées

La moitié de la communauté en IA s’est jetée sur le problème

Le 8 octobre, quelqu’un a battu Cinematch

Le 15 octobre, 3 équipes l’avaient battu, dont 1 de 1,06 %

Le 26 juin 2009, une équipe \no 1 bat Cinematch de 10,05 %
$\rightarrow$ \alert{last call} : plus qu’un mois pour gagner

Le 25 juillet 2009, une \alert{équipe \no 2} bat Cinematch de 10,09 %

L’équipe \no 1 fait 10,09 % aussi

20 minutes plus tard \alert{l’équipe \no 2} fait 10,10 %

… En fait, les deux équipes étaient ex \ae quo sur la validation

… Du coup c’est la première équipe à envoyer ses résultats qui a gagné (équipe 1, 10,09 %)

Confidentialité des utilisateurs

Août 2009, Netflix annonce une saison 2

Entre-temps, en 2007 deux chercheurs de l’université du Texas ont été capables d’\alert{identifier} les utilisateurs du jeu de données anonymisées en croisant les données avec IMDb

(année approximative de naissance, code postal, films vus)

En décembre 2009, 4 utilisateurs de Netflix ont attaqué Netflix en justice

Mars 2010, arrangement à l’amiable, la plainte est close

Informations démographiques

Savoir qui est un garçon ou une fille sur le site : pour ou contre ?

\pause

\alert{Fairness} : s’assurer que l’erreur du modèle ne varie pas trop sur des catégories de population

Il faut mesurer les discriminations pour réduire les inégalités

Allez, on récapitule

Comment ça marche ?

recommander des films $\Rightarrow$ \alert{inférer} des notes qui n’existent pas
\alert{validation croisée} pour comparer les méthodes

$k$ plus proches voisins
factorisation de matrice $\Rightarrow$ apprendre une \alert{représentation}
utiliser l’information présente dans les posters

Quels sont les risques ?

Confidentialité : réidentifier des personnes
Est-ce que le modèle est ouvert ?
Est-ce qu’il aggrave des biais ?

Merci pour votre attention ! \hfill jj@mangaki.fr

\centering {width=45%}\

\alert{mangaki.fr} \hfill Twitter : \alert{@MangakiFR}, @jjvie

\raggedright

Pour en savoir plus

AI for Manga & Anime: \alert{research.mangaki.fr}
Notamment un article sur LinuxMag qui explique comment programmer un algorithme de recommandation en Python

\centering \includegraphics[height=3cm]{figures/styletransfer.jpg}

Minimisation alternée

Trouver \alert{$U_k$} qui minimise $$f(U_k) = \sum_{i, j} (\underbrace{\alert{U_i} \cdot W_j}{prédit} - \underbrace{r{ij}}_{réel})^2 + \underbrace{\lambda

\alert{U_i}

_2^2 + \lambda

W_j

2^2}{régularisation}$$

(au fait : la dérivée de $\alert{u} \cdot v$ par rapport à $\alert{u}$ est $v$)

\pause

Trouver les zéros de $f'(U_k) = \sum_{j \textnormal{ rated by } k} 2 (\alert{U_k} \cdot W_j - r_{kj}) W_j + 2 \lambda \alert{U_k} = 0$ peut s’écrire $A\alert{U_k} = B$ so $\alert{U_k} = A^{-1}B$ (facile)

Complexité : $O(n^3)$ où $n$ est le nombre d’œuvres notées par $U_k$