% Parcours de graphes % Christoph Dürr; Jill-Jênn Vie % SU November Camp\newline 2 novembre 2021 — aspectratio: 169 theme: metropolis mainfont: EBGaramond12-Regular.otf mainfontoptions:

• Path=/home/jj/.local/share/fonts/
• “BoldFont=LinLibertine_RB.otf{=latex}” colorlinks: true header-includes:

• \usepackage{minted}

  Un labyrinthe

\centering \

Parcours main gauche

\centering \

Parcours main gauche ?

\centering \

Parcours en profondeur (DFS) avec une pile {.fragile}

\centering \

from tryalgo.dfs import dfs  # pip install tryalgo
prec = dfs(laby_graph)

Depth-first search {.fragile}

process(node)
    mark this node
    for each neighbor of node
        if neighbor is not marked
	        process(neighbor)

\pause

def dfs_recursive(graph, node, seen):
    seen[node] = True
    for neighbor in graph[node]:
        if not seen[neighbor]:
            dfs_recursive(graph, neighbor, seen)

Depth-first search, iterative {.fragile}

\scriptsize

dfs(node)
    todo |$\gets$| empty stack, then push node to todo
	while todo is not empty
	    node |$\gets$| pop from todo
		mark this node
		for each neighbor of node
		    if neighbor is not marked
			    push neighbor to todo

\pause

def dfs_iterative(graph, start, seen):
    seen[start] = True
    to_visit = [start]
    while to_visit:
        node = to_visit.pop()
        for neighbor in graph[node]:
            if not seen[neighbor]:
                seen[neighbor] = True
                to_visit.append(neighbor)

Parcours en profondeur (DFS) optimal ? {.fragile}

\centering \ \qquad \

from tryalgo.dfs import dfs
prec = dfs(laby_graph)

Parcours en largeur (BFS) avec une file {.fragile}

\centering \ \qquad \

from tryalgo.bfs import bfs
dist, prec = bfs(laby_graph)

Breadth-first search {.fragile}

bfs(node)
	todo |$\gets$| empty queue
	mark node
	push node to todo
	while todo is not empty
	    node |$\gets$| pop from todo
		for each neighbor of node
		    if neighbor is not marked
			    mark neighbor
			    push neighbor to todo

Le graphe de Paris

\centering

\

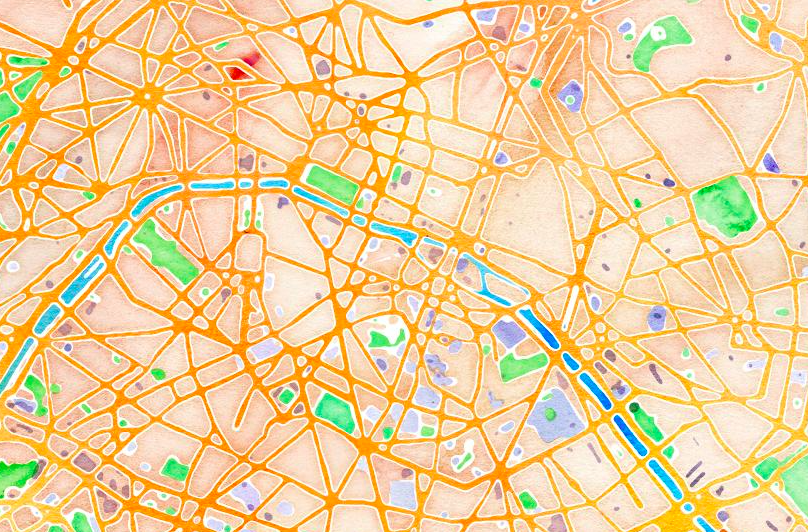Google Hash Code 2014

Énoncé original

• On vous donne \alert{8 voitures} partant de Google Paris sur le graphe de Paris à 11348 intersections, 17958 rues.
• Chaque rue est étiquetée par une \alert{distance} en mètres et un \alert{temps} de parcours en secondes.
• Certaines rues sont à \alert{double sens}, d’autres ne le sont pas.
• Comment explorer un \alert{maximum} de km de Paris en \alert{15 heures} ?

La meilleure solution : graphes eulériens

\centering \

\vspace{1cm}

\raggedright \textbf{Condition :} 0 ou 2 nœuds ayant un nombre \alert{impair} de voisins.

Eulérianiser Paris par des plus courts chemins

\centering \

\vspace{1cm}

\raggedright Certains nœuds ont \alert{trop} d’arcs entrants, d’autres en \alert{manquent}.
\textbf{Idée :} les \alert{coupler} par des \textcolor{blue}{plus courts chemins}.

Références

• TryAlgo Maps in Paris, un notebook Jupyter pour jouer vos algorithmes sur le graphe de Paris
• Pour en savoir plus sur l’épreuve Google Hash Code 2014
  par Antoine Amarilli