% TabDDPM: Modelling Tabular Data with Diffusion Models % Jill-Jênn Vie % MILLE CILS 2023 — aspectratio: 169 institute: \includegraphics[height=1cm]{figures/inria.png} \includegraphics[height=1cm]{figures/soda.png} header-includes:

• \def\E{\mathbb{E}}

Context

Generating synthetic data that follows similar distribution than real data

Potentially with privacy guarantees

Contributions

• TabDDPM for \alert{denoising diffusion probabilistic models} (DDPM) for tabular data with categorical and continuous features
• Outperform GAN and VAE
• More private than a simple counterpart (SMOTE)

Metrics

High ML efficiency

• Average of weak learner should be efficient (good $R^2$) for both real and fake data
• Strong learner (gradient boosting tree) should also have good $R^2$ for both real and fake data

High distance to closest record

To mitigate privacy issues

Low difference between correlation matrices

Baselines

Several GAN-based

SMOTE is a shallow interpolation-based method that “generates” a synthetic point as a convex combination of a real data point and its $k$-th nearest neighbors from the dataset
(originally proposed for minor class oversampling, here for synthetic data generation)

Experiments on 15 real-world public datasets

Results I: High ML efficiency

• Average of weak learner should be efficient (good $R^2$) for both real and fake data

• Strong learner (gradient boosting tree) should also have good $R^2$ for both real and fake data

Results II: High distance to closest record

Results III: Low difference between correlation matrices

\centering

{width=95%}

TabDDPM model

• Continuous variables: Gaussian diffusion model
• Categorical variables: Multinomial diffusion model

What are diffusion models? (Check Lilian Weng’s post!)

\centering

{width=85%}

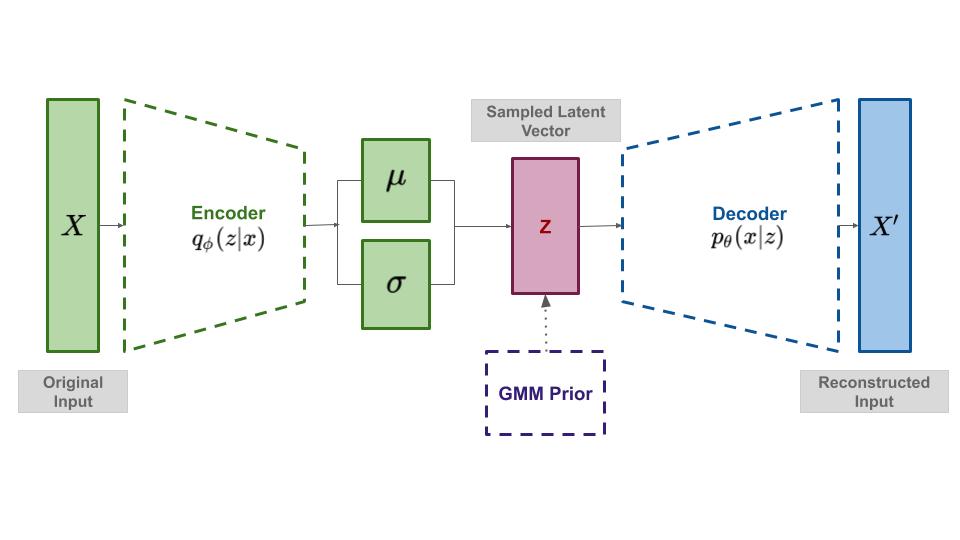
Intro: variational autoencoders

\centering

{width=75%}

\vspace{-1cm}

\raggedright

• Encoder: $x \mapsto z$ with posterior $q_\theta(z

  x) = \mathcal{N}(\mu, \sigma) \simeq p(z

  x)$

• Decoder: $z \mapsto x$ with likelihood $p_\theta(x

  z)$

Kingma, Diederik P and Welling, Max. Auto-Encoding Variational Bayes. In The 2nd International Conference on Learning Representations (ICLR), 2013.

VAE objective

\[\log p(x) \geq \E_{q(z)} \left(\log p(x|z)) - KL(q(z)||p(z))\right)\]

\centering

{width=70%}

\raggedright

Variational Inference: Foundations & Innovations (Blei 2019)

Back to the paper: diffusion model objective

:::::: {.columns} ::: {.column width=60%} \begin{align}\label{eq:elbo} \log q\left(x_0\right) \geq & \mathbb{E}_{q\left(x_0\right)} \big[\underbrace{\log p_{\theta}\left(x_0 | x_1\right)}_{L_0} - \underbrace{KL\left(q\left(x_T|x_0\right) | q\left(x_T\right)\right)}_{L_T} -
& \sum_{t = 2}^T \underbrace{KL\left(q\left(x_{t - 1}|x_t, x_0\right) | p_{\theta}\left(x_{t - 1} | x_t\right)\right)}_{L_t}\big] \end{align} ::: ::: {.column} \includegraphics{figures/DDPM.png} ::: ::::::

:::::: {.columns} ::: {.column}

Continuous are Gaussian

\begin{align} & q\left(x_t | x_{t - 1}\right) := \mathcal{N}\left(x_t; \sqrt{1 - \beta_t}x_{t - 1}, \beta_t I\right)
& q\left(x_T\right) := \mathcal{N}\left(x_T; 0, I\right)
& p_{\theta}\left(x_{t - 1}| x_t\right):= \mathcal{N}\left(x_{t - 1}; \mu_{\theta}\left(x_t, t\right), \Sigma_{\theta}\left(x_t, t\right)\right) \end{align}

Parameterization trick so that the $KL$ becomes $L^2$ over noise variance component. ::: ::: {.column}

Categorical are Multinomial

\begin{align} & q(x_t | x_{t - 1}) := Cat\left(x_t; \left(1 - \beta_t\right)x_{t - 1} + \beta_t / K\right)
& q\left(x_T\right) := Cat\left(x_T; 1/K\right)
& q\left(x_t | x_{0}\right) = Cat\left(x_t; \bar{\alpha}_t x_{0} + \left(1 - \bar{\alpha}_t\right)/ K\right) \end{align}

$q(x_{t - 1}|x_t, x_0)$ has closed form. ::: ::::::

Ethics slide

Because of GDPR this research exists

As even people who are supposed to have access to the data are not having access to the data (non-asymptotically)

Risks of creating whole fake datasets in order to support some claim
(generation of fake datasets conditioned on the results)

\vspace{1cm}

Akim Kotelnikov, Dmitry Baranchuk, Ivan Rubachev, Artem Babenko.
\alert{TabDDPM: Modelling Tabular Data with Diffusion Models.} Proceedings of the 40th International Conference on Machine Learning, PMLR 202:17564-17579, 2023. https://arxiv.org/abs/2209.15421

\vspace{1cm}

Thanks and see you around! jill-jenn.vie@inria.fr