Jill-Jênn Vie

Researcher at Inria

% Variational factorization machines applied to anime/manga recommendations\newline and preference elicitation % Jill-Jênn Vie¹ \and Hisashi Kashima¹² % ¹ RIKEN Center for AIP, Tokyo\newline ² Kyoto University — handout: true theme: Frankfurt section-titles: false header-includes: - \usepackage{bm} - \usepackage{multicol,booktabs} - \usepackage{algorithm,algpseudocode,algorithmicx} - \DeclareMathOperator\logit{logit} - \def\Lb{\mathcal{L}_b} - \def\ReLU{\textnormal{ReLU}} —

Introduction

About France

\includegraphics[width=\linewidth]{figures/france7.jpg}

Outline

Anime/Manga Recommendations (regression)

Modeling pairwise interactions for collaborative filtering
ALS-WR: Alternating Least Squares (Zhou et al., 2008)
Using side information (posters) (V et al., 2017)

Knowledge Tracing (binary classification)

Modeling side information
Item Response Theory (1985)
Factorization Machines (Rendle, 2012)
Deep FMs (Guo et al., 2017)

Variational Training of Factorization Machines

Bayesian FMs
Variational: inference $\rightarrow$ optimization

Recommender Systems

Problem

Every user rates few items (1 %)
How to infer missing ratings?

Example

\begin{tabular}{ccccc} & \includegraphics[height=2.5cm]{figures/1.jpg} & \includegraphics[height=2.5cm]{figures/2.jpg} & \includegraphics[height=2.5cm]{figures/3.jpg} & \includegraphics[height=2.5cm]{figures/4.jpg}
Satoshi & ? & 5 & 2 & ?
Kasumi & 4 & 1 & ? & 5
Takeshi & 3 & 3 & 1 & 4
Joy & 5 & ? & 2 & ? \end{tabular}

Recommender Systems

Problem

Every user rates few items (1 %)
How to infer missing ratings?

Example

\begin{tabular}{ccccc} & \includegraphics[height=2.5cm]{figures/1.jpg} & \includegraphics[height=2.5cm]{figures/2.jpg} & \includegraphics[height=2.5cm]{figures/3.jpg} & \includegraphics[height=2.5cm]{figures/4.jpg}
Satoshi & \alert{3} & 5 & 2 & \alert{2}
Kasumi & 4 & 1 & \alert{4} & 5
Takeshi & 3 & 3 & 1 & 4
Joy & 5 & \alert{2} & 2 & \alert{5} \end{tabular}

Rate anime

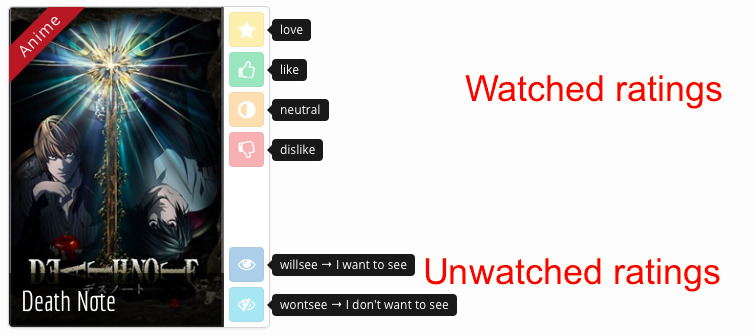Build a profile

Find recommendations

Mangaki data

360000 ratings from 2400 users over 17000 items
Python / Django $\rightarrow$ open source on GitHub
Got a prize from Japan Foundation

Modeling the problem

Fit on existing ratings

\begin{center} \begin{tabular}{ccc} \toprule Kasumi & \alert{like} & \emph{Zootopia}
Kasumi & \alert{favorite} & \emph{Porco Rosso}
Satoshi & \alert{favorite} & \emph{Tokikake}
Satoshi & \alert{dislike} & \emph{The Martian}\ \bottomrule \end{tabular} \end{center}

Predict new user-item pairs

\begin{center} \begin{tabular}{ccc} \toprule Kasumi & \alert{\only<1>{?}\only<2>{favorite}} & \emph{The Martian}
Satoshi & \alert{\only<1>{?}\only<2>{like}} & \emph{Zootopia}\ \bottomrule \end{tabular} \end{center}

Graphically

\includegraphics{figures/svd2black.jpg}

A popular model for collaborative filtering

Approximate $R$ ratings $n \times m$

\alert{$U$} user vectors $n \times d$
\alert{$V$} item vectors $m \times d$.

\[R \simeq \alert{UV^T}\]

\begin{block}{Fit} Learn $U$ and $V$ to \alert{minimize} $ {||R - UV^T||}_2^2 + \lambda \cdot \textnormal{regularization} $ \end{block}

\pause

\begin{block}{Predict: Will user Satoshi like item Naruto?} Just compute $\alert{U_{\textnormal{Satoshi}}} \cdot \alert{V_{\textnormal{Naruto}}}$ and you will know! \end{block}

Alternating Least Squares (Zhou et al., 2008)

\begin{algorithm}[H] Initialize randomly $U$ and $V$ \begin{algorithmic} \Repeat \State Fix users $U$ learn items $V$ to minimize error + reg \State Fix items $V$ learn users $U$ \Until {convergence} \end{algorithmic} \caption{Alternating Least Squares with Weighted Regularization} \label{als-wr} \end{algorithm}

\fullcite{zhou2008large}

Graphically running ALS-WR (orange: users, blue: items)

\includegraphics{figures/embed38.pdf}

Our implementations are on \url{github.com/mangaki/zero}

\centering 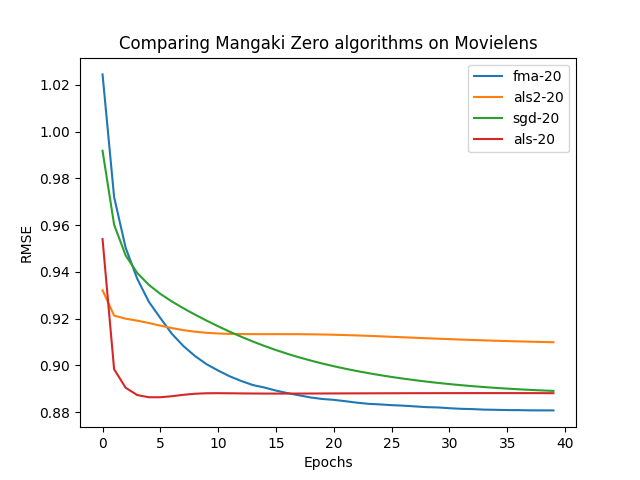{width=80%}\

\pause

\alert{N. B.} – FMA does not mean Fullmetal Alchemist
FMA means Factorization Machine

Drawback with collaborative filtering: Cold-Start

If no ratings are available for a work $j$
$\Rightarrow$ Its vector $W_j$ cannot be learned :-(

$\Rightarrow$ No way to distinguish between unrated works.

But we have (many) posters!

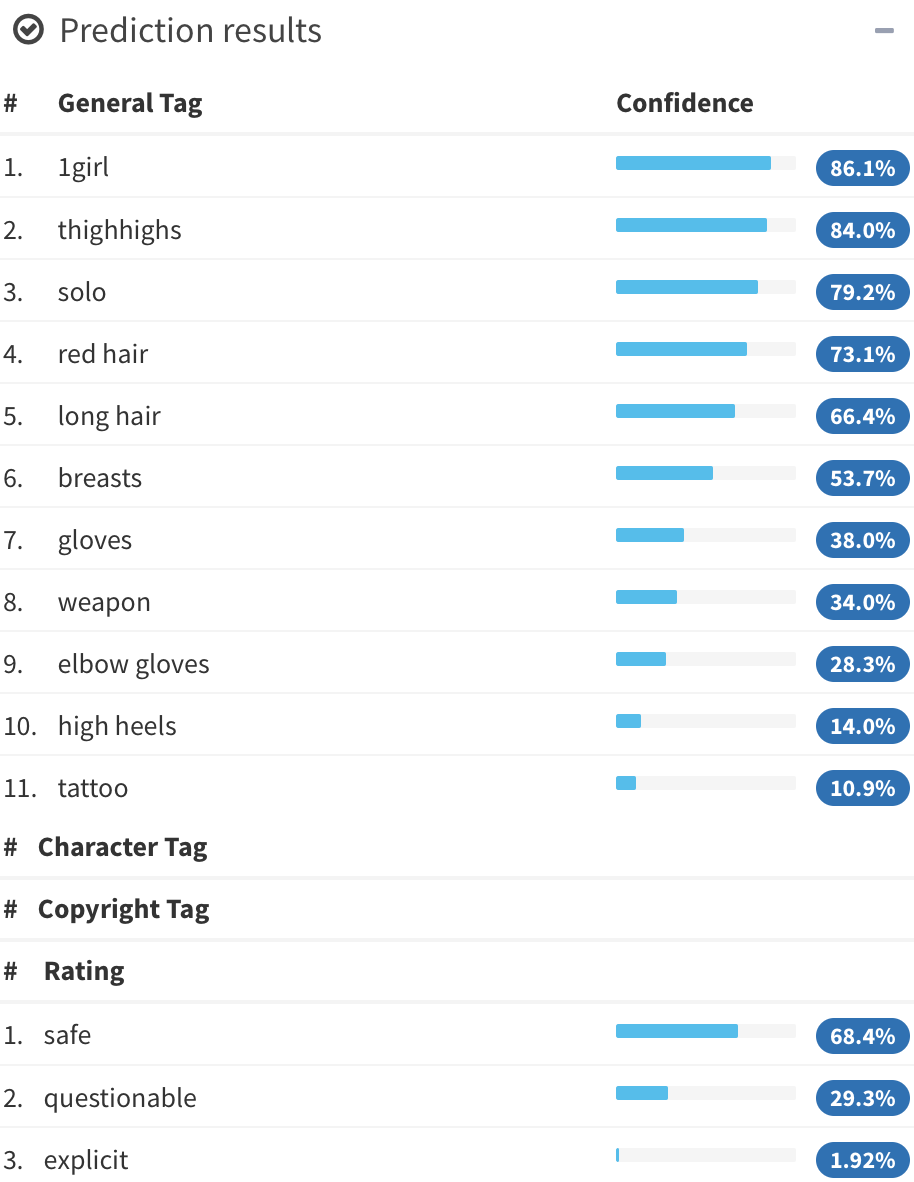
Illustration2Vec (Saito and Matsui, 2015)

\centering

{height=70%}\ {height=70%}\

CNN (VGG-16) pretrained on ImageNet (photos)
Retrained on Danbooru (1.5M manga illustrations with tags)
502 most frequent tags kept, outputs \alert{tag weights}

Blended Alternate Least Squares with Explanation

\includegraphics{figures/archifinal.pdf}

Published in MANPU workshop in ICDAR 2017

From the reviewers: \bigskip

\pause

Two models individually are existing methods, but this work presents a novel fusion method called \alert{Steins gate} to integrate results given by two models.

\fullcite{BALSE2017}

FMs for Item Response Theory

A new problem setting: knowledge tracing

Fit

Existing student $i$ got question $j$ correct or incorrect

Predict

Will student $i$ get question $j$ correct?

Graphically

\centering \includegraphics[width=0.49\linewidth]{figures/embedding1.png}

Side information

User: country, days, client (desktop, mobile), session, format, time
Item: gender, part of speech

Duolingo data

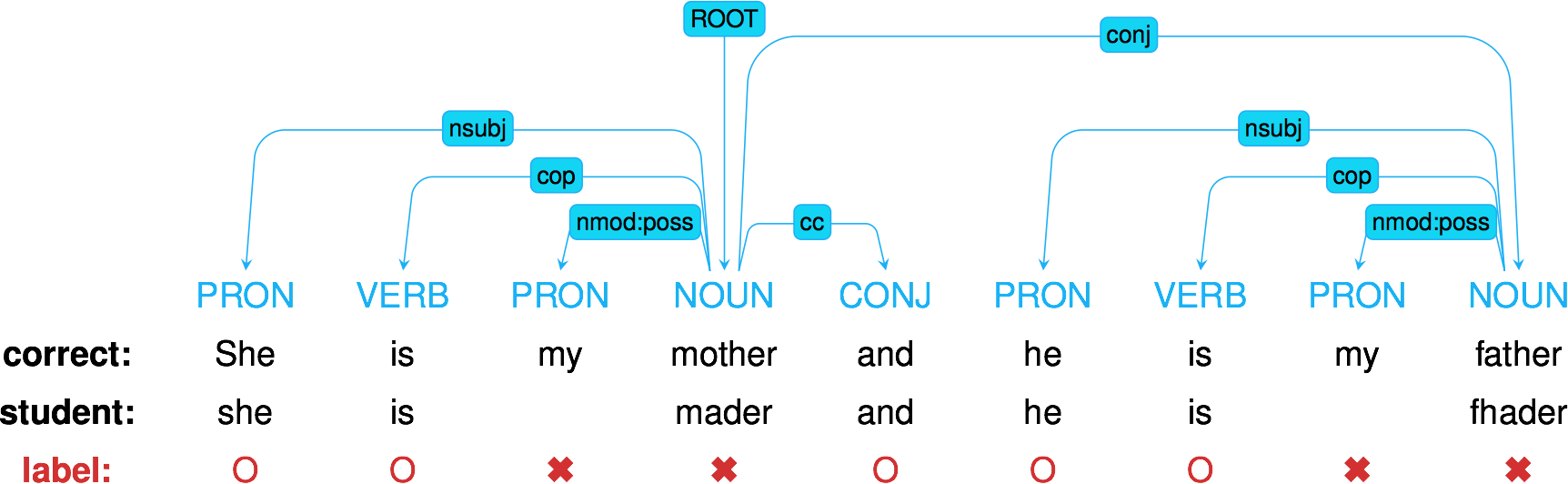
One simple model: Item Response Theory

Learn abilities $\theta_i$ for each user $i$
Learn easiness $e_j$ for each item $j$ such that: $\begin{aligned} Pr(\textnormal{User $i$ Item $j$ OK}) & = \sigma(\theta_i + e_j)\\ \logit Pr(\textnormal{User $i$ Item $j$ OK}) & = \theta_i + e_j \end{aligned}$

Intuition

If user $i$ is \alert{strong} (high $\theta_i$)
$\rightarrow$ they have higher chance to solve any question
If question $j$ is \alert{easy} (high $e_j$)
$\rightarrow$ anyone has higher chance to solve it

\pause

Logistic regression

Learn $\alert{\bm{w}}$ such that $\logit Pr(\bm{x}) = \langle \alert{\bm{w}}, \bm{x} \rangle$

Usually with L2 regularization: ${

\bm{w}

}_2^2$ penalty $\leftrightarrow$ Gaussian prior

Graphically: IRT as logistic regression

\centering

\[Pr(\textnormal{User $i$ Item $j$ OK}) = \sigma(\langle \bm{w}, \bm{x} \rangle) = \sigma(\theta_i + e_j)\]

How to model side information?

If you know user $i$ attempted item $j$ on \alert{mobile} (not desktop)
How to model it?

$y$: score of event “user $i$ solves correctly item $j$”

IRT

\[y = \theta_i + e_j\]

Multidimensional IRT

\[y = \theta_i + e_j + \langle \bm{v_{\textnormal{user $i$}}}, \bm{v_{\textnormal{item $j$}}} \rangle\]

\pause

With side information

\[y = \theta_i + e_j + \langle \bm{v_{\textnormal{user $i$}}}, \bm{v_{\textnormal{item $j$}}} \rangle + \langle \bm{v_{\textnormal{user $i$}}}, \alert{\bm{v_{\textnormal{mobile}}}} \rangle + \langle \bm{v_{\textnormal{item $j$}}}, \alert{\bm{v_{\textnormal{mobile}}}} \rangle\]

Encoding the problem using sparse features

\centering \input{tables/show-swf}

Graphically: factorization machines

\centering

Formally: factorization machines

Learn bias \alert{$w_k$} and embedding \alert{$\bm{v_k}$} for each feature $k$ such that: $\logit p(\bm{x}) = \mu + \underbrace{\sum_{k = 1}^N \alert{w_k} x_k}_{\textnormal{logistic regression}} + \underbrace{\sum_{1 \leq k < l \leq N} x_k x_l \langle \alert{\bm{v_k}}, \alert{\bm{v_l}} \rangle}_{\textnormal{pairwise interactions}}$

\fullcite{rendle2012factorization}

Training using, for example, SGD

Take a batch $x_{batch}$ and $y_{batch}$ and update the parameters such that the error is minimized.

Error in classification:
cross-entropy, log loss, negative log-likelihood
Error in regression: RMSE

\begin{algorithm}[H] \begin{algorithmic} \For {batch $\bm{X}_B, y_B$} \For {$k$ feature involved in this batch $\bm{X}_B$} \State Update $w_k, \bm{v}_k$ to decrease loss estimate $\mathcal{L}$ on $\bm{X}_B$ \EndFor \EndFor \end{algorithmic} \caption{SGD} \label{algo-vfm} \end{algorithm}

Why do we prefer distributions over point estimates?

Because we measure \alert{uncertainty}
More robust for critical applications
Can guide sequential estimation (preference elicitation)

Training using MCMC

\begin{algorithm}[H] Prior on every $V$ \begin{algorithmic} \For {each iteration} \State Sample hyperparameters from posterior using MCMC \State Sample weights $w$ \State Sample vectors $V$ \State Sample predictions $y$ \EndFor \end{algorithmic} \caption{MCMC implementation of FMs} \label{mcmc-fm} \end{algorithm}

MCMC require many samples to converge

\fullcite{rendle2012factorization}

Deep Factorization Machines

Learn layers \alert{$W^{(\ell)}$} and \alert{$b^{(\ell)}$} such that: $\begin{aligned}[c] \bm{a}^{0}(\bm{x}) & = (\alert{\bm{v_{\texttt{user}}}}, \alert{\bm{v_{\texttt{item}}}}, \alert{\bm{v_{\texttt{device}}}}, \ldots)\\ \bm{a}^{(\ell + 1)}(\bm{x}) & = \ReLU(\alert{W^{(\ell)}} \bm{a}^{(\ell)}(\bm{x}) + \alert{\bm{b}^{(\ell)}}) \quad \ell = 0, \ldots, L - 1\\ y_{DNN}(\bm{x}) & = \ReLU(\alert{W^{(L)}} \bm{a}^{(L)}(\bm{x}) + \alert{\bm{b}^{(L)}}) \end{aligned}$

\[\logit p(\bm{x}) = y_{FM}(\bm{x}) + y_{DNN}(\bm{x})\]

\fullcite{guo2017deepfm}

Experiments: Duolingo

\fullcite{Settles2018}

Duolingo dataset

\centering \input{tables/duolingo}

Available on \url{http://sharedtask.duolingo.com}

Duolingo ranking

\centering

\begin{tabular}{cccc} \toprule Rank & Team & Algo & AUC\ \midrule 1 & SanaLabs & RNN + GBDT & .857
2 & singsound & RNN & .854
2 & NYU & GBDT & .854
4 & CECL & LR + L1 (13M feat.) & .843
5 & TMU & RNN & .839\ \midrule 7 (off) & JJV & Bayesian FM & .822
8 (off) & JJV & DeepFM & .814
10 & JJV & DeepFM & .809\ \midrule 15 & Duolingo & LR & .771\ \bottomrule \end{tabular}

\raggedright \fullcite{Duolingo2018}

Variational Training

Variational inference

Approximate true posterior with an easier distribution (Gaussian)
according to the KL divergence

Idea

We want to increase some objective which is intractable
$\textnormal{objective} \geq \underbrace{\textnormal{easyobjective} - \textnormal{KLdivergence}}_{\textnormal{ELBO: Evidence Lower Bound}}$\bigskip

Increase the ELBO $\Rightarrow$ increase the objective

Graphically: VFM

VFM training

\begin{algorithm}[H] \begin{algorithmic} \For {batch $\bm{X}_B, y_B$} \For {$k$ feature involved in this batch $\bm{X}_B$} \State Sample $w_k \sim q(w_k)$, $\bm{v}_k \sim q(\bm{v}_k)$ \EndFor \For {$k$ feature involved in this batch $\bm{X}_B$} \State Update each* parameter $\theta$ to increase an unbiased ELBO estimate $\Lb$ on this batch $\bm{X}_B$ \EndFor \EndFor \end{algorithmic} \caption{Variational Training (SGVB) of FMs} \label{algo-vfm} \end{algorithm}

* Here, $\theta \in {\mu_k^w, \sigma_k^w, \bm{\mu}_k^v, \bm{\sigma}_k^v}$

Experiments

Data

\centering \input{tables/datasets-movies}

Models

libFM ALS implementation
libFM MCMC implementation
ALS-WR
VFM
VFM+si: VFM plus side information

Movielens

\scriptsize \begin{table}[h] \centering \input{tables/table-sep-4-forced} \caption{Results on all datasets for the regression task.} \label{results} \end{table}

Fraction

\tiny \begin{table} \centering \input{tables/table-sep-5b} \caption{Results on the Fraction dataset for the classification task.} \label{results-class} \end{table}

Conclusion

FMs are a better baseline than logistic regression when side information is abundant
But noisy side information degrades performance

\vspace{1cm}

Variational training speeds up training
and can make better inference
Notably useful in large datasets

Thanks for listening!

VFM is implemented in TensorFlow.

Feel free to try it on GitHub (vfm.py):

github.com/jilljenn/vae

\vspace{1cm}

Please try Mangaki:

mangaki.fr