Jill-Jênn Vie
Researcher at Inria
% Programme ta culture ! % Jill-Jênn Vie % 7 mars 2017 — header-includes: - \usepackage{tikz} - \usepackage{array} - \usepackage{icomma} - \usepackage{multicol,booktabs} - \def\R{\mathcal{R}} handout: true —
Hi, I’m JJ
- 2012 Président de Prologin
- 2014 Agrégé de mathématiques + Girls Can Code! + Mangaki
- 2016 Docteur en informatique + 2 livres d’algorithmique
- Programmation efficace (concours de programmation) w/ Dürr
- Les clés pour l’info (concours des ENS) w/ Mansuy, Belghiti
- 2017 Postdoc à RIKEN Tokyo
Recommandation de films
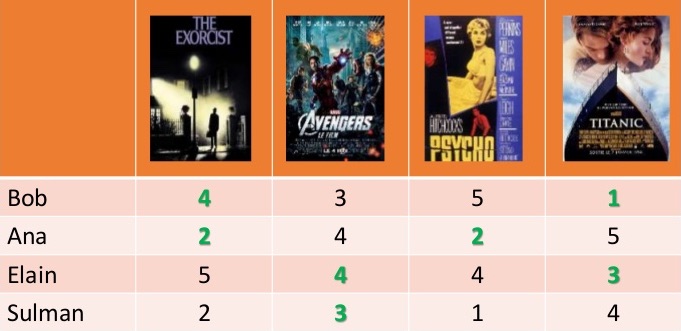
Problème
- Chaque utilisateur note peu de films (1 %)
- Comment inférer les notes manquantes ?
 \
\
Cartographie des goûts
Problème
Comment mettre un nom sur les goûts de l’utilisateur ?
Exemple
Votre corps est composé à 80 % d’eau, à 10 % de Woody Allen, à 10 % de films noirs.
Élicitation des préférences
Problème
Comment faire un diagnostic des goûts de l’utilisateur ?
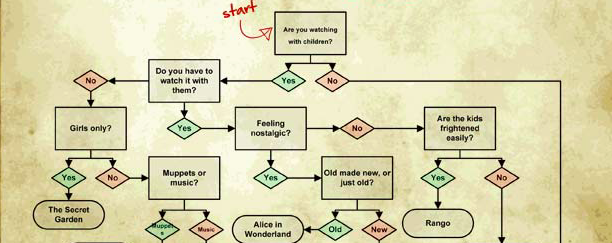 \
\
\centering \em \small What to Watch on Netflix, Silver Oak Casino, 2013
Jeu de données 1 : Movielens
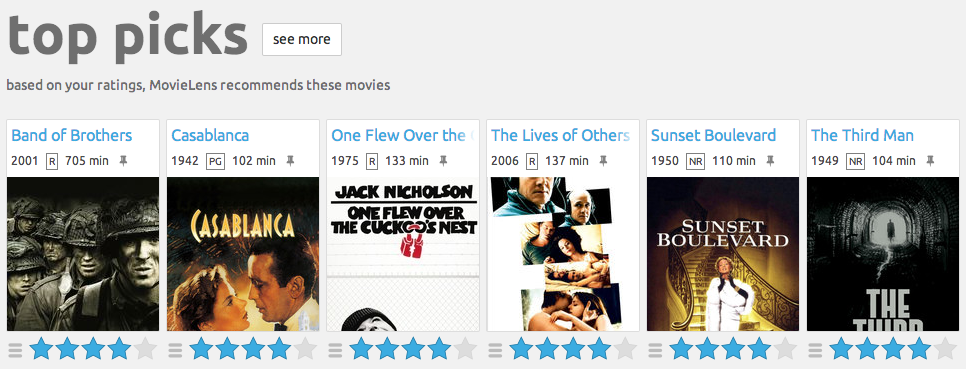 \
\
- 700 utilisateurs
- 9000 films
- 100000 notes
Jeu de données 2 : Mangaki
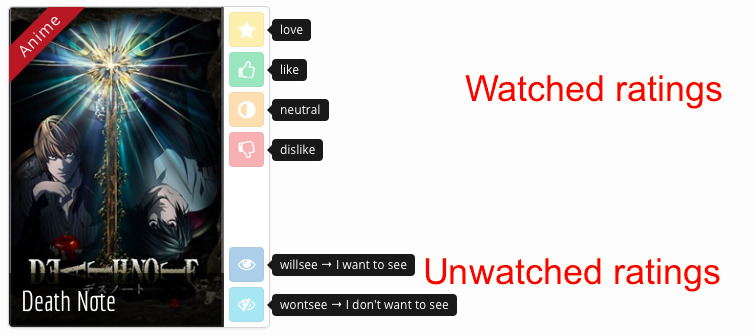 \
\
- 2100 utilisateurs
- 15000 œuvres \textcolor{gray}{\hfill {\em \small anime / manga / OST}}
- 310000 notes \textcolor{gray}{\hfill {\em \small fav / like / dislike / neutral / willsee / wontsee}}
- Un utilisateur note quelques œuvres \textcolor{gray}{\hfill {\em \small Élicitation des préférences}}
- Et reçoit des recommandations \textcolor{gray}{\hfill {\em \small Filtrage collaboratif}}
Tout algorithme de machine learning supervisé
fit($X$, $y$)
\centering
\begin{tabular}{ccc} \toprule
\multicolumn{2}{c}{$X$} & $y$\ \cmidrule{1-2}
\texttt{user_id} & \texttt{work_id} & \texttt{rating}\ \midrule
24 & 823 & like
12 & 823 & dislike
12 & 25 & favorite
\ldots & \ldots & \ldots\ \bottomrule
\end{tabular}
\pause
$\hat{y}$ = predict($X$)
\centering
\begin{tabular}{ccc} \toprule
\multicolumn{2}{c}{$X$} & $\hat{y}$\ \cmidrule{1-2}
\texttt{user_id} & \texttt{work_id} & \texttt{rating}\ \midrule
24 & 25 & \only<2>{?}\only<3>{\alert{disliked}}
12 & 42 & \only<2>{?}\only<3>{\alert{liked}}\ \bottomrule
\end{tabular}
Évaluation : RMSE
Si je prédis $\hat{y}$ pour chacun des $n$ paires à évaluer,
alors que la vérité est $y^*$ :
KNN $\rightarrow$ mesurer la similarité
$K$ plus proches voisins
- Score de similarité entre utilisateurs : \(score(u, v) = \frac{\R_u \cdot \R_v}{||\R_u|| \cdot ||\R_v||}.\)
- Identifions les $k$ plus proches voisins d’un utilisateur
- Recommandons-lui ce que ses voisins ont aimé qu’il n’a pas vu
Astuce
| Si $R$ est la matrice $N \times M$ des $\frac{\R_u}{ | \R_u | }$, alors pour obtenir la matrice des scores entre utilisateurs $N \times N$ il suffit de calculer $R R^T$. |
PCA, SVD $\rightarrow$ réduire la dimension
Analyse de composantes principales, déc. en valeurs singulières
\vspace{-7mm}
\(R = \left(\begin{array}{c} \R_1\\ \R_2\\ \vdots\\ \R_n \end{array}\right) = \raisebox{-1cm}{\begin{tikzpicture} \draw (0,0) rectangle (2.5,2); \end{tikzpicture}} = \raisebox{-1cm}{\begin{tikzpicture} \draw (0,0) rectangle ++(1,2); \draw node at (0.5,1) {$C$}; \draw (1.1,1) rectangle ++(2.5,1); \draw node at (2.35,1.5) {$P$}; \end{tikzpicture}}\) Chaque ligne $\R_u$ est une combinaison linéaire des profils $P$.
\pause
Profils types
\begin{tabular}{@{}lccc@{}}
Si $P$ & $P_1$ : aventure & $P_2$ : romance & $P_3$ : plot twist
Et $C_u$ & $0,2$ & $-0,5$ & $0,6$
\end{tabular}
$\Rightarrow$ $u$ \alert{aime un peu} l’aventure, \alert{déteste} la romance, \alert{adore} les plot twists.
\vspace{2mm}
\pause
$R = (U \cdot \Sigma)V^T$ où $U : N \times r$ et $V : M \times r$ sont orthogonales et $\Sigma : r \times r$ diagonale.
ALS-WR $\rightarrow$ variantes
Moindres carrés alternés avec régularisation pondérée
Rappel : $R$ notes, $C$ coefficients, $P$ profils.
$R = CP = CF^T$ i.e. $r_{ij} \simeq C_i \cdot F_j$.
L’erreur de reconstruction est minimisée
SVD : $\sum_{i, j}~(r_{ij} - C_i \cdot F_j)^2$ (vaut 0 si $r$ est égal au rang)
\pause
ALS : $\sum_{i, j \textnormal{\alert{ connus}}}~(r_{ij} - C_i \cdot F_j)^2$
\pause
| ALS-WR : $\sum_{i, j \textnormal{\alert{ connus}}}~(r_{ij} - C_i \cdot F_j)^2 + \lambda (\sum_i N_i | C_i | ^2 + \sum_j M_j | F_j | ^2)$ |
\pause
| WALS by Tensorflow™ : $$\sum_{i, j} w_{ij} \cdot (r_{ij} - C_i \cdot F_j)^2 + \lambda (\sum_i | C_i | ^2 + \sum_j | F_j | ^2)$$ |
\pause
À votre avis, qui gagne ?
NMF $\rightarrow$ interpréter les composantes
Non-negative matrix factorization
On suppose $R$, $C$ et $F \geq 0$.
| NMF : $\sum_{i, j}~(r_{ij} - C_i \cdot F_j)^2 + \lambda (\sum_i | C_i | ^2 + \sum_j | F_j | ^2)$ |
Avantage
Les composantes sont plus facilement interprétables.
Arbre de décision
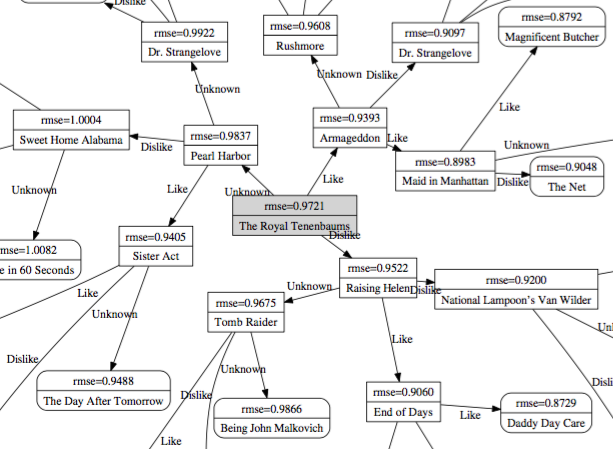 \
\
Bon équilibre entre likes, dislikes et « ne sait pas »
Comment poser des bonnes questions ?
Si on a quelques vecteurs de $F$ :
\centering
\
Interprétation géométrique de la diversité
\centering
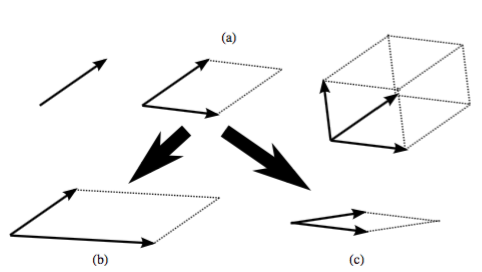 \
\
- Déterminant = carré du volume du parallélotope formé
- Vecteurs peu corrélés (\alert{diversifiés}) augmentent le volume
- On souhaite échantillonner $k$ éléments parmi $n$ efficacement
DPP : pour modéliser la diversité
Processus à point déterminantal
\centering
points \alert{éloignés les uns des autres}
=
films \alert{diversifiés}
 \
\
DPP
On souhaite échantillonner $n$ œuvres
$K : n \times n$ \alert{matrice de similarité} sur les œuvres (semi-définie positive)
$P$ est un \alert{processus à point déterminantal} si l’échantillon $Y$ vérifie : \(\forall A \subset \{1, \ldots, n\}, \quad P(A \subseteq Y) \propto det(K_A) = Vol(\{x_i\}_{i \in A})^2\)
Il existe un algo en $O(nk^3)$ pour échantillonner $k$ parmi $n$ !
Exemple
\begin{columns}
\begin{column}{0.5\textwidth}
[ K = \left(\begin{array}{cccc}
1 & 2 & 3 & 4
2 & 5 & 6 & 7
3 & 6 & 8 & 9
4 & 7 & 9 & 1
\end{array}\right) ]
\end{column}
\begin{column}{0.5\textwidth}
$A = {1, 2, 4}$ sera inclus dans la sélection avec probabilité
[ K_A = det\left(\begin{array}{ccc}
1 & 2 & 4
2 & 5 & 7
4 & 7 & 1
\end{array}\right) ]
\end{column}
\end{columns}
SAE
Avec SVD, on passe d’une représentation des gens en dimension $M$ films à une représentation en dimension $r$, qui est censée suffire à décrire leurs notes.
\pause
Ça ne vous fait pas penser à quelque chose ?
\pause
\begin{center} \includegraphics[height=4cm]{figures/sae.png} Sparse autoencoder! \end{center}
Une petite anecdote
- Le 2 octobre 2006, Netflix a lancé un concours :
Le premier qui bat notre algorithme de plus de 10 % remportera 1 million de dollars.
et ont filé des données anonymisées- La moitié de la communauté en IA s’est jetée sur le problème
- Le 8 octobre, quelqu’un a battu Cinematch
- Le 15 octobre, 3 équipes l’avaient battu, dont 1 de 1,06 %
- Le 26 juin 2009, une équipe 1 bat Cinematch de 10,05 %
$\rightarrow$ \alert{last call} : plus qu’un mois pour gagner- Le 25 juillet 2009, une \alert{équipe 2} bat Cinematch de 10,09 %
- L’équipe 1 fait 10,09 % aussi
- 20 minutes plus tard \alert{l’équipe 2} fait 10,10 %
- … En fait, les deux équipes étaient ex \ae quo sur le sous-ensemble de validation
- … Du coup c’est la première équipe à envoyer ses résultats qui a gagné (équipe 1, 10,09 %)
Confidentialité des utilisateurs
- Août 2009, Netflix annonce une saison 2
- Entre-temps, en 2007 deux chercheurs de l’université du Texas ont été capables d’\alert{identifier} les utilisateurs du jeu de données anonymisées en croisant les données avec IMDb
- (année approximative de naissance, code postal, films vus)
- En décembre 2009, 4 utilisateurs de Netflix ont attaqué Netflix en justice
- Mars 2010, arrangement à l’amiable, la plainte est close
Programme ta culture !
Initiation à la programmation à la création numérique
(option ICN au lycée séries L, ES et S)
Activités
- Exploration de données massives
- Création artistique numérique
- Recommandation de films
tryalgo.org/programme-ta-culture
Quelle série voir, finalement ?
\begin{tabular}{cccl}
\Large Données & \raisebox{-2cm}{\includegraphics[width=2.5cm]{figures/bm.jpg}} & \raisebox{-2cm}{\includegraphics[width=2.5cm]{figures/kaiba.jpg}} & \small \em Kaiba
\Large Chat \& souris & \raisebox{-2cm}{\includegraphics[width=2.5cm]{figures/sherlock.jpg}} & \raisebox{-2cm}{\includegraphics[width=2.5cm]{figures/fujiko.jpg}} & \parbox{2cm}{\small \em Lupin the Third: The Woman Called Fujiko Mine}
\end{tabular}
Merci de votre attention !
\centering
 \
\
\raggedright
Retrouvez ces slides
Sur research.mangaki.fr
Retrouvez le code
Sur GitHub : github.com/mangaki
Suivez-nous
Sur Twitter : @mangakifr